Ортогональное проецирование

Параллельное проецирование называется ортогональным (прямоугольным), если направление проецирования s перпендикулярно к плоскости проекций П′ (s^П’).

В ортогональной проекции очень просто устанавливать соотношение между длиной натурального отрезка и длиной его проекции.

Пусть отрезок АВ образует с плоскостью проекций П' угол f (рисунок 1.2.5). Проведём A^′ В₁параллельно АВ. Тогда

А'В'=А'В₁× cos j=АВ× cos j

Большое распространение ортогональные проекции получили в технических чертежах, т.к. позволяют особенно легко судить о размерах изображаемых предметов.

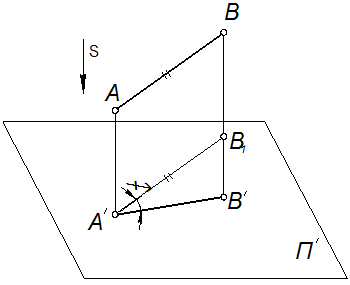
Рисунок 1.2.5 – Ортогональное проецирование

1.2.4 Образование двух- и трёхкартинного комплексного чертежа

Наиболее употребительным в практике является метод комплексного чертежа в ортогональных проекциях. Комплексным чертежом называется чертёж, состоящий из нескольких связанных между собой проекций изображаемой фигуры. Метод комплексного чертежа в ортогональных проекциях называется такжеметодом Монжа.

Этот метод прост в построении и даёт большую точность при графическом решении задач. Он обеспечивает точное определение изображённой фигуры по чертежу. Недостатком метода является малая наглядность изображений.

Комплексный чертёж из двух проекций называется также двухкартинным чертежом.

Рассмотрим неподвижную систему двух взаимно перпендикулярных плоскостей П₁ и П₂ в соответствии с рисунком 1.2.6. Плоскость П₁, расположенная горизонтально, называется горизонтальной плоскостью проекций. Плоскость П₂, перпендикулярная к П₁, занимает вертикальное положение и расположена перед наблюдателем. Эту плоскость называют фронтальной плоскостью проекций. На обе эти плоскости будем проецировать ортогонально точки пространства.

Предположим, что в пространстве имеется некоторая точка А. Ортогональную проекцию А₁ точки А на плоскость П₁ будем называть горизонтальной проекцией точки А, а ортогональную проекцию А₂ точки А на плоскость П₂ -фронтальной проекцией точки А. Прямые АА₁ и АА₂, при помощи которых точка А проецируется на плоскости проекций (AА₁^П₁, AА₂^П₂), называются проецирующими прямыми (AА₁ – горизонтально проецирующая прямая, АА₂ – фронтально проецирующая прямая). Прямая пересечения плоскостей проекций называется осью проекций. Её обозначают буквой x.

Плоскость, перпендикулярную к плоскости проекций, называют проецирующей плоскостью (плоскость, перпендикулярная к плоскости П₁, называется горизонтально проецирующей плоскостью, а плоскость, перпендикулярная к плоскости П₂, – фронтально проецирующей плоскостью).

Плоскость АА₁А₂ проходит через прямую АА₁, перпендикулярную к плоскости П₁, в силу чего она перпендикулярна к плоскости П₁. Аналогично плоскость АА₁А₂ перпендикулярна плоскости П₂. Следовательно, дважды проецирующая плоскость АА₁А₂ перпендикулярна к оси проекций X.

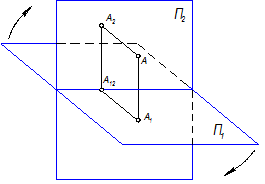Точку пересечения плоскости АА₁А₂ с осью проекций х как точку, принадлежащую одновременно обеим плоскостям П₁ и П₂, обозначим А₁₂. Прямые A₁₂А₁ и А₁₂А₂, лежащие в плоскости АА₁А₂, перпендикулярной к оси проекций х, перпендикулярны к этой оси. Обратно, пусть А₁₂ - произвольная точка оси проекций х. Восставим из точки А₁₂ к оси два перпендикуляра: один в плоскости П₁, другой в плоскости П₂.

Рисунок 1.2.6 – Ортогональное проецирование точки

Тогда каждая пара точек А₁ и А₂, лежащих на этих перпендикулярах, определит в пространстве единственную точку А. Действительно, две пересекающиеся прямые А₁₂А₁ и А₁₂А₂ определяют плоскость А₁А₁₂А₂, перпендикулярную к оси проекций х (так как А₁₂А₁^х и А₁₂А₂^х). Но плоскость, перпендикулярная к линии х пересечения двух плоскостей П1 и П₂, перпендикулярна к каждой из этих плоскостей, т.е. плоскость А₁А₁₂А₂ является проецирующей по отношению к обеим плоскостям проекций. Следовательно, перпендикуляры, восставленные в точках А₁ и А₂ соответственно к плоскостям П₁ и П₂, лежат в одной плоскости (в плоскости А₁А₁₂А₂). Точка А их пересечения и является искомой точкой пространства, определяемой данной парой точек Итак, каждой точке А соответствует пара её проекций А₁ и А₂, лежащих вместе с данной точкой А в одной плоскости, перпендикулярной к обеим плоскостям проекций П₁ и П₂, а следовательно, и к линии х их пересечения; обратно, любые две точки А₁ÎП₁ и А₂ÎП₂, лежащие в одной плоскости, перпендикулярной к оси х, определяют в пространстве единственную точку А.

Расстояние А₁А точки А от горизонтальной плоскости проекций называется высотойточки А, а её расстояние А₂А от фронтальной плоскости проекций – глубиной точки А.

Для получения плоского чертежа совмещаем плоскость проекций П₁ с плоскостью П₂ путем вращения плоскости П₁ вокруг оси X в направлении, указанном на рисунке 1.2.6 стрелками, так, чтобы передняя полуплоскость П₁ совместилась с нижней полуплоскостью П₂. В результате получим комплексный чертёжточки А (рисунок 1.2.7), состоящий из двух проекций А₁ и А₂ точки А. Обе проекции А₁ и А₂ лежат на одном перпендикуляре к оси проекций х, которую как прямую, принадлежащую одновременно обеим плоскостям проекций П₁ и П₂, будем обозначать на комплексном чертеже х₁₂. Два перпендикуляра А₁₂А₁ и А₁₂А₂ к оси х₁₂ имеют общую точку А₁₂. Прямая А₁А₂, соединяющая две проекции точки на комплексном чертеже, называется линией связи. Линия связи двух проекций точки перпендикулярна к оси проекций.

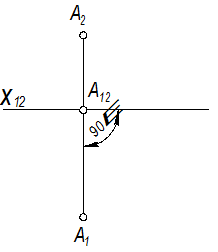ПРИМЕЧАНИЕ:контуры плоскостей проекций на комплексном чертеже не показывают.

Рисунок 1.2.7 – Комплексный чертёж точки

Плоскости проекций разбивают всё пространство на четыре части, называемые квадрантами или четвертями. Принято нумеровать квадранты в порядке, указанном на рисунке 1.1.8, и называть их I, П, Ш, IV квадрантами.

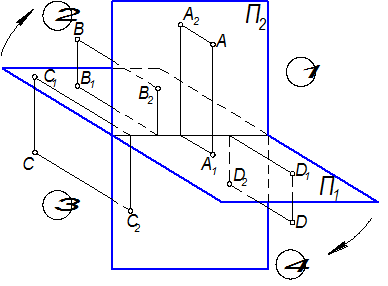
Рисунок 1.2.8 – Квадранты пространства

Если точка лежит в I квадранте, то её горизонтальная проекция А₁, будет принадлежать передней полуплоскости П₁, а фронтальная проекция А₂ – верхней полуплоскости П₂. При совмещении плоскостей проекций горизонтальная проекция А₁ точки А, лежащей в I квадранте, окажется расположенной ниже оси x₁₂ в соответствии с рисунком 1.2.9.

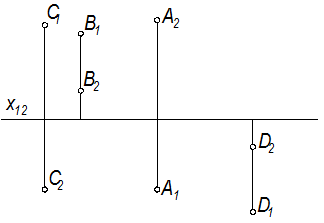В зависимости от положения натуральных (проецируемых) точек в различных квадрантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже в соответствии с рисунком 1.2.9, так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит натуральная точка.

Рисунок 1.2.9 – Комплексный чертёж точек, расположенных в разных квадрантах

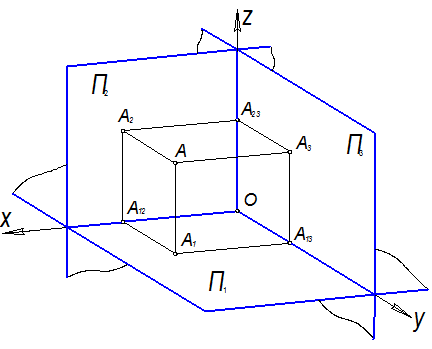
Двухкартинный чертёж является метрически определённым чертежом. Однако, в силу трёхмерности пространственной фигуры её комплексный чертёж становится более ясным, когда, помимо двух основных проекций, дана ещё одна проекция на третью плоскость. В качестве такой плоскости проекций чаще всего применяют профильную плоскость проекций П₃ (рис. 1.2.10).

П₃^х, поэтому П₃^П₁ и П₃^П₂. Три плоскости проекций (П₁, П₂, П₃) образуют в пространстве прямоугольный трёхгранник, т.е. систему трёх взаимно перпендикулярных плоскостей. Ребра трёхгранника обозначим через х, y, z.

Пусть А – некоторая точка пространства. Для определения положения точки А относительно системы плоскостей (П₁, П₂, П₃) опустим из точки А перпендикуляры на плоскости проекций: AA_i^П_i (i=l, 2, 3). Основания этих пер-пендикуляров (точки А₁, А₂, А₃) и являются соответственногоризонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций (П₁, П₂, П₃). Проецирующие плоскости AA₁A₂, AA₁A₃ и АА₂А₃ перпендикулярны соответственно к осям х, у, z. Обозначим точки пересечения этих плоскостей с осями через А₁₂, А₁₃, А₂₃. Как прямые A₁A₁₂ и A₁₂A₂ перпендикулярны к оси x, так и две другие пары прямых A₁A₁₃, A₁₃A₃ и А₂А₂₃, А₂₃А₃ должны быть перпендикулярны соответственно к осям y и z. Расстояние точки А от профильной плоскости проекций П₃ называется широтойточки А.

Рисунок 1.2.10 – Трёхкартинный чертёж точки

Итак, A₁A=A₁₂A₂=A₁₃A₃– высота, А₂А=А_]2А₁=А₂₃A₃ – глубина, АзА=А₂₃A₂=A₁₃A₁ – широта точки А.

При построении плоского чертежа плоскость П₂ считается неподвижной, а плоскости П₁и П₃совмещаются с ней путём вращения соответственно вокруг осей х и z в направлении, в соответствии с рисунком 1.2.10. После совмещения плоскости П₁ с фронтальной плоскостью П₂ отрезки А₁А₁₂^x₁₂ и А₁₂А₂^x₁₂ окажутся расположенными на одной прямой. Аналогично после совмещения плоскости П₃ с плоскостью П₂ отрезки А₂А₂₃^z₂₃ и А₂₃А₃^z₂₃ расположатся на линии связи А₂А₃^z₂₃.

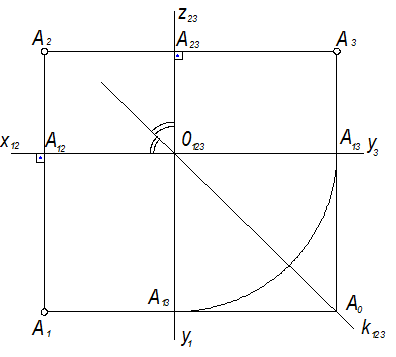Рисунок 1.2.11 – Трёхпроекционный комплексный чертёж точки

В результате указанного совмещения плоскостей проекций получаем комплексный чертёж точки А в трёх ортогональных проекциях. При этом линии связи должны быть перпендикулярны к осям А₁А₂^x₁₂, А₂А₃^z₂₃, а отрезки А₁₂А₁ и А₂₃А₃ равны, так как А₁₂А₁₌А₂₃А₃=А₂А (рисунок 1.1.11) есть глубина точки А.

Рассмотрим квадрат А₁₃O₁₂₃А₃₁А₀. Диагональ этого квадрата является биссектрисой угла (Х₁₂Z₂₃_).Следовательно, линия связи, соединяющая проекции А₁ и А₂, представляет собой ломаную линию с вершиной на биссектрисе К₁₂₃угла (X₁₂Z₂₃), состоящую из двух звеньев (горизонтального и вертикального). Часть этой ломаной заменяют иногда дугой окружности.

Таким образом, линии связи устанавливают на трёхкартинном чертеже следующим образом: А₁А₂ – вертикальная линия связи; А₂А₃ – горизонтальная линия связи; А₁А₃ – горизонтально-вертикальная линия связи; биссектриса К₁₂₃ – геометрическое место вершин ломаных линий связи в соответствии с рисунком 1.2.12.

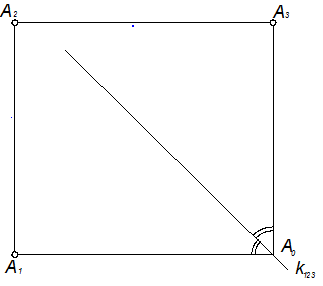
Рисунок 1.2.12 – Линии связи на проекционном чертеже

Прямая К₁₂₃ определяется заданием трёх проекций какой-либо точки, например, точки А (А₁А₂А₃), и является постоянной прямой комплексного чертежа.

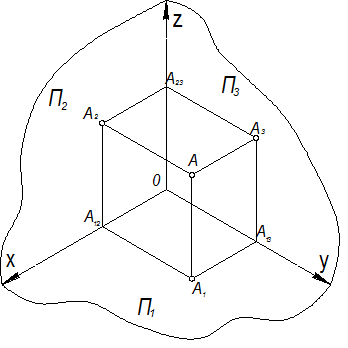Рассмотрим трёхгранник, образованный системой плоскостей проекций (П₁,П₂,П₃). На осях x, y, z установим единицу измерения е. За начало отсчёта примем точку О пересечения трёх плоскостей проекций (вершину трёхгранника). Положительное направление на каждой оси установим, как показано на рисунке 1.2.13. Тогда трёхгранник Оxyz можно рассматривать как прямоугольную декартову систему координат с координатными осями: Ох – ось абсцисс, Оy – ось ординат, Оz – ось аппликат с координатными плоскостями хОyºП₁, хОzºП₂, yОzºП₃..

Рисунок 1.2.13 – Прямоугольная система координат в пространстве

Точку А(x_A, y_A, z_A) по данным координатам х_А,,y_A_,z_A строят следующим образом: пользуясь единицей длины е, строим отрезок АА₁₂, затем отрезок А₁₂А₁, параллельный оси у, и отрезок А₁А, параллельный оси z. В результате получаем точку А(х_А, у_А, z_А).

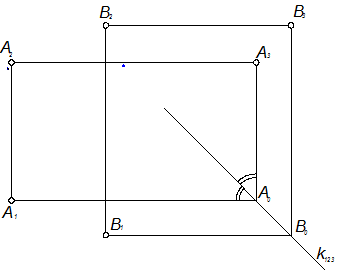На чертежах, применяющихся в технике, оси проекций обычно не показывают. Это означает, что плоскости проекций могут перемещаться параллельно самим себе. Однако, и при отсутствии на чертеже осей всегда можно определить по данным двум проекциям точки третью её проекцию, если на чертеже имеются три проекции хотя бы одной точки. Это достигается при помощи постоянной прямой k чертежа, являющейся биссектрисой угла, образованного ломаной линией связи в соответствии с рисунком 1.2.14. Например, известно расположение трёх проекций точки А. Это позволяет определить постоянную k₁₂₃ как биссектрису угла А₁А₀А₃. В результате линии связи становятся вполне определёнными и по каждым двум проекциям точки может быть построена третья её проекция. На рисунке 1.2.14 такое построение выполнено для точки В.

Рисунок 1.2.14 – Безосный комплексный чертёж точки

<1 234 5 6 7 >

Дата добавления: 2016-06-02; просмотров: 1796;