Колебаний. Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w. Меха­нические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равнове-сия, либо зарядом (Q) конденсатора.

Из формулы (18.52) следует, что ампли-туда А смещения (заряда) имеет максимум при некоторой частоте w_рез., называемой резонан-сной. Таким образом, чтобы определить резонансную частоту w_рез. нужно найти максимум функции (18.52), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкорен­ное выраже-ние по w и приравняв его нулю, получим условие, определяющее w_рез.:

.

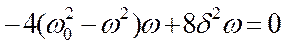Это равенство выполняется при w=0, 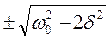, у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота

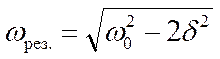. (18.54)

Резонансом (соответственно механичес-кимили электрическим) называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуж-дающей силы (частоты вынуждающего пере-менного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, При d²<<w₀² значение w_рез. практи-чески совпадает с собственной частотой w₀ колебательной системы. Подставляя (18.54) в формулу (18.52), получим

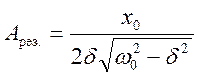. (18.55)

На рис.18.12 приведе-ны зависимости ампли-туды вынужденных ко-лебаний от частоты при различных значениях d. Из (18.54) и (18.55) вы-текает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w®0, то все кривые (см. также (18.52)) достигают одного и того же, отличного от нуля, предельного значения х₀/w₀², которое называют статическим отклонением. В случае механических колебаний х₀/w₀²=F₀/(mw₀²), а в случае электромагнитных — U_m/(Lw₀²)Если w®¥, то все кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы (18.55) вытекает, что при малом затухании (d²<<w₀²) резонансная амплитуда смещения (заряда)

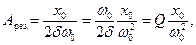
где q - добротность колебательной системы (см. (18.44)), х₀/w₀²— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А_рез..

Из выражения tgj=2dw/(w₀²-w²) (см. (18.53)) следует, что если затухание в системе отсутствует (d=0), то только в этом случае колебания и вынуждающая сила (прило­женное переменное напряжение) имеют одинаковые фазы; во всех других случаях j¹0.

Зависимость j от w при разных коэффи-циентах d графически представлена на рис.18.13, из которого следует, что при изме-нении w изменяется и сдвиг фаз j. Из фор-мулы (18.53) вытекает, что при w=0 j=0, а при w=w₀ независимо от значения коэффициента затухания j=p/2, т.е. сила (напряжение) опережает по фазе колебания на p/2. При дальнейшем увеличении w сдвиг фаз возрас-тает и при w>>w₀ j®p, т.е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кри-вых, изображенных на рис.18.13, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так радиотехника, прикладная акустика, электротехника используют явление резонанса.

18.10. Переменный ток

Переменный ток – это установившиеся вынужденные электромагнитные колебания протекающие в цепи, содержащей резистор, катушку индуктивности и конденсатор. Переменный ток можно считать квазистацио-нарным, если изменения мгновенных значе-ний силы тока во всех сечениях цепи прак-тически одинаковы и происходят достаточно медленно в сравнении с электромагнит­ными возмущения, распространяющимися по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных то-ков выполняются закон Ома и вытека­ющие из него правила Кирхгофа, которые будут испо-льзованы применительно к пере­менным токам.

Рассмотрим последовательно процессы, происходящие на участке цепи, содер­жащем резистор, катушку индуктивности и конденса-тор, к концам которого приложено перемен-ное напряжение

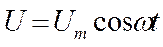. (18.56)

где U_m — амплитуда напряжения.

1. Переменный ток, текущий через резистор сопротивлением R (L®0, С®0) (рис.18.14,а). При выполнении условия квазистационарности ток через резистор опреде­ляется законом Ома:

, '

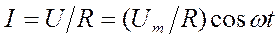где амплитуда силы тока .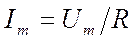

Для наглядного изображения соотношений между переменными токами и напряже-ниями воспользуемся методом векторных диаграмм. На рис.18.14,б дана векторная
диаграмма амплитудных значений тока I_m и напряжения U_m на резисторе (сдвиг фаз
между I_m и U_m равен нулю).

2. Переменный ток, текущий через катушку индуктивностью L (R®0, С®0)ис.18.15,а). Если в цепи приложено перемен-ное напряжение (18.56), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции

.

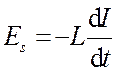Тогда закон Ома для рас-сматриваемого участка цепи имеет вид

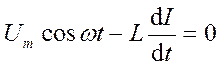
откуда

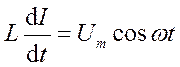. (18.57)

Так как внешнее напряжение приложено к катушке индуктивности, то

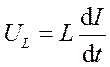(18.58)

есть падение напряжения на катушке. Из уравнения (18.57) следует, что

;

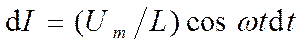после интегрирования, учитывая, что постоян-ная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим

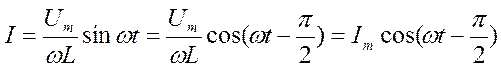, (18.59)

где 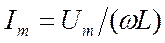. Величина

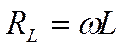(18.60)

называется реактивным индуктивным соп-ротивлением (или индуктивным сопротив-лением).

Из выражения (18.60) вытекает, что для постоянного тока (w=0) катушка индуктив-ности не имеет сопротивления. Подстановка значения U_m=wLI_mв выражение (18.57) с учетом (18.58) приводит к следующему значению падения напряжения на катушки индуктивности:

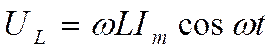
. (18.61)

Сравнение выражений (18.59) и (18.61) приводит к выводу, что падение напряжения
U_L опережает по фазе ток I, текущий через катушку, на p/2, что и показано на
векторной диаграмме (рис.18.15, б).

3. Переменный ток, текущий через конденсатор емкостью С (R®0, L®0). (рис.18.16,а). Если переменное напряжение (18.56) приложено к конденсато-ру, то он все время перезаряжае-тся, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конден-сатору, а сопротивлением подво-дящих проводов можно пренебречь, то

.

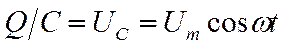Сила тока

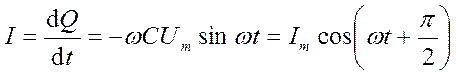, (18.62)

где

.

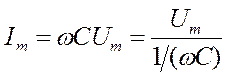Величина

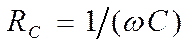
называется реактивным емкостным сопро-тивлением (или емкостным сопротивле-нием).

Для постоянного тока (w=0) R_C=¥, т.е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

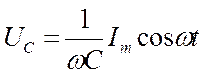. (18.63)

Сравнение выражений (18.62) и (18.63) приводит к выводу, что падение напряжения U_C отстает по фазе от текущего через конденсатор тока I на p/2. Это показано на векторной диаграмме (рис.18/16, б).

4. Цепь переменного тока, содержащая последовательно включенные резистор, ка­тушку индуктивности и конденсатор. На рис.18.17,а представлен участок цепи, содер­жащий резистор сопро-тивлением R, катушку индуктивностью L и конденсатор ем­костью С, к концам которого приложено переменное напряжение (18.56). В цепи возникнет пере-менный ток, который вызовет на всех элементах цепи соответству-ющие падения напряжения U_R, U_L и U_c. На рис.18.17,б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R)» катушке (U_L) и конденсаторе (U_C). Амплитуда U_m приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис.18.17,б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что

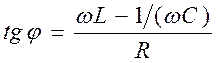_. (18.64)

Из прямоугольного треугольника получаем 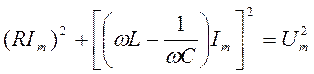, откуда амплитуда силы тока имеет значение

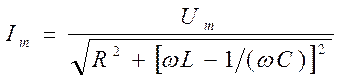. (18.65)

Следовательно, если напряжение в цепи изменяется по закону U=U_mcoswt, то в цепи течет ток

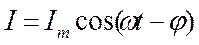, (18.66)

где j и I_m определяются соответственно формулами (18.64) и (18.65). Величина

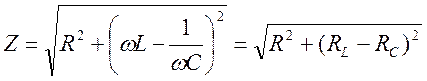(18.67)

называется полным сопротивлением цепи, а величина

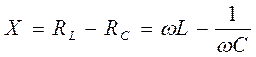
- реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_Rи U_L в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис.18.18, из которого следует, что

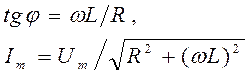. (18.68)

Выражения (18.64) и (18.65) совпадают с (18.68), если в них 1/(wС)=0, т.е. С=¥. Следовательно, отсутствие конденсатора в цепи означает С=¥,а не С=0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстоя­ние между обкладками стремится к нулю, а емкость — к бесконечности).