Вынужденные колебания

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:

.

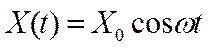Если рассматривать механические колеба-ния, то роль X(t)играет внешняя вынуж­дающая сила

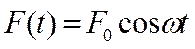(18.45)

Учетом (18.45) закон движения для пружинного маятника можно записать в виде дифференциального уравнения

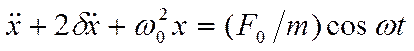. (18.46)

Если рассматривать электрический колеба-тельный контур, то роль X(t)играет подводи-мая к контуру внешняя периодически изменя-ющаяся по гармоническому закону э.д.с. или переменное напряжение

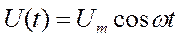. (18.47)

Тогда дифференциальное уравнение про-цессов, происходящих в колебательном кон-туре с учетом (18.47) можно записать в виде

,

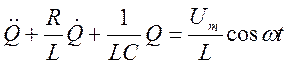Или после преобразования

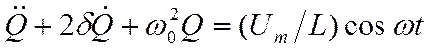. (18.48)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с, называются соответственно вынужден-ными механическими и вынужденными электромагнитными колебаниями.

Уравнения (18.46) и (18.48) можно свести к линейному неоднородному дифференци­альному уравнению

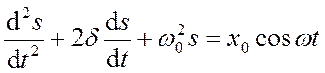, (18.49)

применяя впоследствии его решение для вынужденных колебаний конкретной физии-чес­кой природы (х₀в случае механических колебаний равно F₀/m, в случае электромаг-нит­ных —U_m/L).

Решение уравнения (18.49) равно сумме общего решения (18.42)

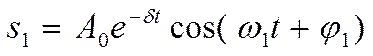(18.50)

однородного урав­нения (18.41)

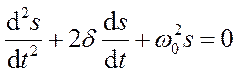
и частного решения

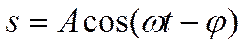(18.51)

неоднородного уравнения (18.49), где ампли-туда и фаза вынужденных колебаний соответственно равны

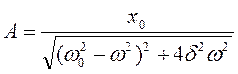, (18.52)

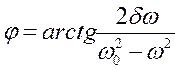. (18.53)

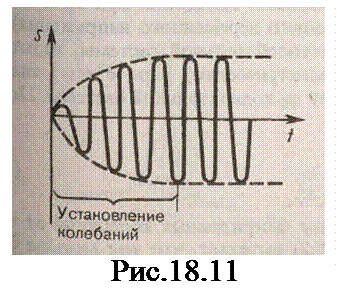Слагаемое (18.50) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не дости-гнет значения, определяемого равенством (18.52). Графически вынужденные колебания представлены на рис.18.11. Следовательно, в установившемся режи-ме вынужденные коле-бания происходят с частотой w и являют­ся гармоническими; амп-литуда и фаза коле-баний, опрделяемые выражениями (18.52) и (18.53), также зависят от w .