5 страница. и показывает, что тело будет совершать гармонические колебания.
и показывает, что тело будет совершать гармонические колебания.
Дифференциальные уравнения делятся на "обыкновенные", содержащие
производные одной или нескольких функций одного независимого
переменного, и "уравнения с частными производными", содержащие частные
производные функций нескольких независимых переменных. Порядком Д. у.
называется наибольший порядок входящих в него производных. Так,
например,
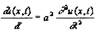
|
есть дифференциальное уравнение с частными производными 2-го порядка.
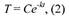
|
Обыкновенные дифференциальные уравнения. Уравнения 1-го порядка.
Обыкновенным дифференциальным уравнением 1-го порядка с одной
неизвестной функцией (только такие пока будут рассматриваться) называется
соотношение
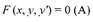
|
| между независимым переменным х, искомой функцией y и её производной |
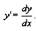
|
| Если уравнение (А) может быть разрешено относительно производной, то получается уравнение вида |
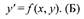
|
Многие вопросы теории дифференциальных уравнений проще рассматривать
для таких разрешённых относительно производной уравнений, предполагая
функцию f(х, у) однозначной.
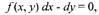
|
| тогда оно становится частным случаем уравнений вида |
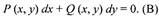
|
Уравнение (Б) можно записать в виде соотношения между дифференциалами
В уравнениях вида (В) естественно считать переменные хиу
равноправными, т. е. не интересоваться тем, какое из них является
независимым.
Геометрическая интерпретация дифференциальных уравнений.
Пусть у=у(х) есть решение уравнения (Б). Геометрически это значит,
что в прямоугольных координатах касательная к кривой у=у(х) имеет в
каждой лежащей на ней точке М (х, у) угловой коэффициент k =f(х, у). Т. о.,
нахождение решений у=у(х) геометрически сводится к такой задаче: в
каждой точке некоторой области на плоскости задано "направление",
требуется найти все кривые, которые в любой своей точке М имеют
направление, заранее сопоставленное этой точке. Если функция f (х, у)
непрерывна, то это направление меняется при перемещении точки М
непрерывно, и можно наглядно изобразить поле направлений, проведя в
достаточно большом числе достаточно густо расположенных по всей
рассматриваемой области точек короткие чёрточки с заданным для этих
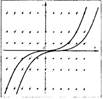
точек направлением. На рис.1 это выполнено для уравнения у'- у2. Рисунок
позволяет сразу представить себе, как должны выглядеть графики решения -
так называемые интегральные кривые Д. у. Вычисление показывает, что
общее решение данного уравнения есть
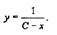
|
На рис 1. вычерчены интегральные кривые,
соответствующие значениям параметра С = 0 и С = 1.
График любой однозначной функции у=у(х)
пересекает каждую прямую, параллельную оси Оу,
только один раз. Таковы, следовательно, интегральные
кривые любого уравнения (Б) с однозначной
непрерывной функцией в правой части. Новые
возможности для вида интегральных кривых открываются при переходе к
уравнениям (В). При помощи пары непрерывных функций Р (х, у) и Q (х, у)
можно задать любое непрерывное "поле направлений". Задача
интегрирования уравнений (В) совпадает с чисто геометрической (не
зависящей от выбора осей координат) задачей разыскания интегральных
кривых по заданному на плоскости полю направлений. Следует заметить, что
тем точкам (х0, у0), в которых обе функции Р (х, у) и Q (х, у) обращаются в
нуль, не соответствует какое-либо определённое направление. Такие точки
называются особыми точками уравнения (В).
Пусть, например, задано уравнение
которое можно записать в виде
|
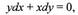
|
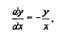
|
хотя, строго говоря, правая часть этого последнего уравнения теряет смысл
при х = 0 и у = 0. Соответствующие поле направлений и семейство
интегральных кривых, являющихся в этом случае окружностями х2 +у2 = С,
изображены на рис.2 . Начало координат (х = 0,y = 0) - особая точка данного
уравнения.
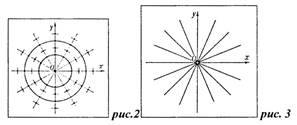
|

|
изображёнными на рис. 3, являются всевозможные прямолинейные лучи,
выходящие из начала координат; начало координат является особой точкой и
этого уравнения.
Начальные условия. Геометрическая интерпретация дифференциальных
уравнений 1-го порядка приводит к мысли, что через каждую внутреннюю
точку М области G с заданным непрерывным полем направлений можно
провести одну вполне определённую интегральную кривую.
В отношении существования интегральной кривой сформулированная
гипотеза оказывается правильной. Например, если для рассмотренного выше
уравнения (1) потребовать, чтобы в начальный момент времени t0 = 0
температура тела была равна "начальному" значению Т0, то из бесконечного
семейства решений (2) выделится одно определённое решение,
удовлетворяющее заданным начальным условиям:
Этот пример типичен: в механике и физике дифференциальные уравнения
обычно определяют общие законы течения какого-либо явления; однако,
чтобы получить из этих законов определённые количественные результаты,
надо присоединить к ним сведения о начальном состоянии изучаемой
физической системы в некоторый определённый выбранный в качестве
"начального" момент времени t0.
Если условия единственности выполнены, то решение у (х),
удовлетворяющее условию у (х0) -у(), можно записать в виде:
где x0 и у0 входят как параметры, функция же j (х; х0, у0) трёх переменных х,
x0 и у0 однозначно определяется самим уравнением (Б). Важно отметить, что
при достаточно малом изменении поля (правой части дифференциальных
уравнений) функция j(x; х0, у0) меняется сколь угодно мало на конечном
промежутке изменения переменного х - имеется непрерывная зависимость
решения от правой части дифференциальных уравнений. Если правая часть f
(х, у) дифференциальных уравнений непрерывна и её производная по у
ограничена, то имеет место также непрерывность j (х; х0, у0) по х0 и у0.
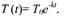
|
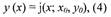
|
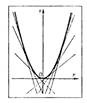
Если в окрестности точки (х0 ,у0) для уравнения (Б) выполнены условия
единственности, то все интегральные кривые, проходящие через достаточно
малую окрестность точки (х0 ,у0), пересекают вертикальную прямую х = х0 и
определяются ординатой у = С своей точки пересечения с этой прямой (см.
рис. 4). Т. о., все эти решения содержатся в семействе с одним параметром С:
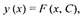
|
|
которое является общим решением дифференциальных уравнений (В).
рис. 4
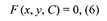
|
| дифференцируют (6) при постоянном С и получают |
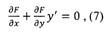
|
Общий интеграл. Особые решения. Естественно поставить
обратную задачу: задано семейство кривых, зависящих от
параметра С, требуется найти дифференциальные уравнения,
для которого кривые заданного семейства служили бы
интегральными кривыми. Общий метод для решения этой
задачи заключается в следующем: считая семейство кривых
на плоскости хОу заданным при помощи соотношения
Дифференциальные уравнения высших порядков и системы
дифференциальных уравнений.
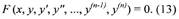
|
| Если ввести дополнительные неизвестные функции |
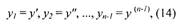
|
Дифференциальные уравнения п-го порядка с одной неизвестной функцией у
(х) независимого переменного х записывают так:
то уравнение (13) можно заменить системой из n уравнений с n
неизвестными функциями, но зато 1-го порядка. Для этого достаточно к n - 1
уравнениям (14) присоединить уравнение
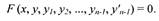
|
Аналогичным образом сводятся к системам уравнений 1-го порядка и
системы уравнений высших порядков. В механике сведение систем
уравнений 2-го порядка к системе из удвоенного числа уравнений 1-го
порядка имеет простой механический смысл. Например, система трёх
уравнений движения материальной точки
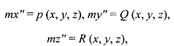
|
где х, у, z - координаты точки, зависящие от времени t, сводится к системе
шести уравнений:
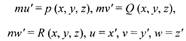
|
при помощи введения в качестве новых переменных составляющих u, v, w
скорости.
Наибольшее значение имеют системы, в которых число уравнений равно
числу неизвестных функций. Система из n уравнений 1-го порядка с n
неизвестными функциями, разрешённая относительно производных, имеет
вид:
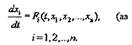
|
Решением системы дифференциальных уравнений (а) называется система
функций x1(t),x2 (t),..., xn(t), которая при подстановке в уравнения (а)
обращает их в тождества.
Задача
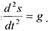
|
| По условию задачи |
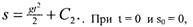
|
| Интегрируем это уравнение; |
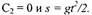
|
| следовательно, |
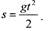
|
| Ответ: |
Ускорение свободного падения тела равно g — тело падает из состояния
покоя. Найти зависимость пути, проходимого телом, от времени: s = f(t).
Решение.
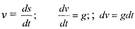
|
| Скорость |
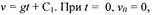
|
| Интегрируем: |
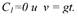
|
| следовательно, |
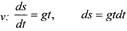
|
| Подставляем значение |
Дифференциальные уравнения с частными производными.
Типичной особенностью дифференциальных уравнений с частными
производными и систем дифференциальных уравнений с частными
производными является то, что для однозначного определения частного
решения здесь требуется задание не значений того или иного конечного
числа параметров, а некоторых функций.
Дифференциальными уравнениями описывают различные процессы в
физике, химии и биологии. Они позволяют, в частности, определять
изменение состояния систем со временем.
Уравнения с частными производными содержат неизвестную функцию (u)
нескольких независимых переменных (например, х у, z) и ее частные
производные. Например, волновое уравнение
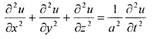
|
Примеры и задачи с решениями
Пример.
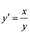
|
| при условии, что у = 4 при х — 2. |
Решить уравнение
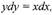
|
| Разделяем переменные: |
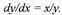
|
| Переписываем: |
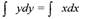 Определяем С:
Определяем С:
|
Интегрируем:
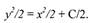
|
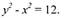
|
| Ответ: |
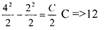
|

| Пример. Решить уравнение Разделяем переменные: Интегрируем выбираем в виде |
| Потенцируем: Определяем С: Ответ: = 2.x. |
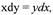
|
| учитывая, что y= 10 при х = 5. |

|

| (постоянную интегрирования для удобства |
Пример.
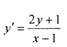
|
Найти общее решение уравнения .
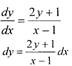
|
| то уравнение имеет вид: |
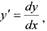
|
| Так как |
| Домножив всё уравнение на dx, получим: |
Решение.
Разделив всё уравнение на (2х +1), приходим к уравнению с
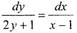
|
| разделяющимися переменными : |
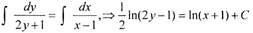
|
| Интегрируя, получим : |
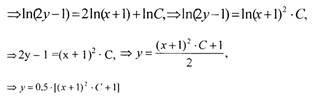 Ответ:
Ответ:
|
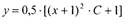
|
Пример.
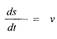
|
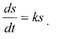
|
| Учитывая условие задачи, можем написать |

| Интегрируем: |
| Задача Найти время, в течение которого масса лекарственного препарата в каком- либо органе уменьшается вдвое вследствие химического распада. Решение. |
Найти общее решение уравнения
Разделяем переменные:
Задача
Найти закон движения тела, движущегося со скоростью, пропорциональной
пройденному пути.

| Интегрируем |
| Ответ: |
Решение.
В начальный момент (t = 0) в органе масса препарата m0. В некоторый
текущий момент t масса не распавшегося препарата равна m За время dt
распалась достаточно малая масса dm препарата. Логично предположить, что
dm пропорционально времени, в течение которого происходил химический
распад: dm = -λmdt,

| Проинтегрируем это дифференциальное уравнение |
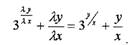 Сделаем подстановку:
Сделаем подстановку:
|
где λ—некоторая постоянная, зависящая от природы препарата,
внешних условий и т. п.; знак «-» означает уменьшение со временем массы
препарата.
Разделим переменные в последнем уравнении:
учитывая, что нижние пределы соответствуют начальным условиям, а
верхние — условию задачи:
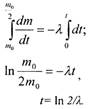 откуда
откуда
|
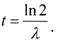
|
| Ответ: |
Пример.
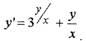
|
| Найти общее решение уравнения |
Решение.
Уравнение является однородным, так как функция, стоящая в правой части,
является однородной:
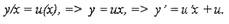
|
Преобразуем исходное уравнение:
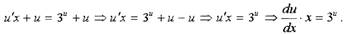 Получили уравнение с разделяющимися переменными:
Получили уравнение с разделяющимися переменными:
|
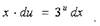
|
Делим уравнение на
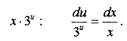
|
Интегрируя почленно, получим:
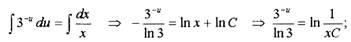
|
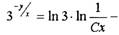
|
общий интеграл.
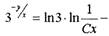
|
| общий интеграл. |
Ответ:
ПРИЛОЖЕНИЕ
Действия с корнями
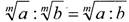
|
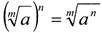
|
1.Величина корня не изменится, если его показатель увеличить в п раз и
одновременно возвести подкоренное значение в степень п:
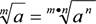
|
2.Величина корня не изменится, если показатель степени уменьшить в п
раз и одновременно извлечь корень п-й степени из подкоренного значения:
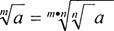
|
3. Корень из произведения нескольких сомножителей равен произведению
корней той же степени из этих сомножителей:
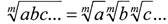
|
Обратно, произведение корней одной и той же степени равно корню той же степени из произведения подкоренных значений:
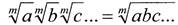
|
4.Корень от частного равен частному от деления корня из делимого на корень из делителя (показатели корней должны быть одинаковыми):
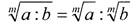
|
Обратно:
5.Чтобы возвести корень в степень, достаточно возвести в эту степень
подкоренное значение:
Обратно, чтобы извлечь корень из степени, достаточно возвести в эту
степень корень из основания степени:
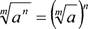
|
Действия со степенями
1.Степень произведения двух или нескольких сомножителей равна
произведению степеней этих сомножителей с тем же показателем:
Практически более важно обратное преобразование:
т.е. произведение одинаковых степеней нескольких величин равно той же
степени произведения этих величин.
2.Степень частного (дроби) равна частному от деления той же степени
делимого на ту же степень делителя:
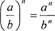
|
3.При умножении степеней с одинаковыми основаниями показатели
степеней складываются:
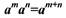
|
4.При делении степеней с одинаковыми основаниями показатель степени
делителя вычитается из показателя степени делимого:
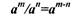
|
5. При возведении степени в степень показатели степеней
перемножаются:
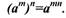
|
Основные тригонометрические формулы
Определение тригонометрических функций для острых
|
углов
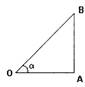
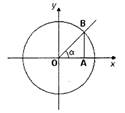
Пусть ОАВ — треугольник с углом α. Тогда:
• Синус - отношение ординаты конца
подвижного радиуса к длине этого радиуса. Синусом α
называется отношение АВ/ОВ (противолежащего катета
к гипотенузе).
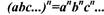
|
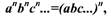
|
• Косинус - отношение абсциссы конца
подвижного радиуса к длине этого радиуса. Косинусом α
называется отношение ОА/ОВ (прилежащего катета к
гипотенузе).
• Тангенс - отношение ординаты конца подвижного радиуса к его
абсциссе. Тангенсом α называется отношение АВ/ОА (отношение
противолежащего катета к прилежащему).
• Котангенс - отношение абсциссы конца подвижного радиуса к его
ординате. Котангенсом α называется отношение ОА/АВ (отношение
прилежащего катета к противолежащему).
• Секанс - отношение длины подвижного радиуса к абсциссе его конца.
Секансом α называется отношение ОВ/ОА (гипотенузы к прилежащему
катету).
• Косеканс - отношение длины подвижного радиуса к ординате его
конца. Косекансом α называется отношение ОВ/АВ (гипотенузы к
противолежащему катету).
• Линия тангенсов - касательная к единичной окружности в конце
горизонтального диаметра.
|
• Линия котангенсов - касательная к единичной окружности в
конце вертикального диаметра.
На рисунке представлена декартова система
координат на плоскости и построена окружность
радиуса R с центром в начале координат О.
Углы измеряются как повороты от
положительного направления оси абсцисс
до луча ОВ.
Направление против часовой стрелки считается
положительным.
Направление по часовой стрелке считается
отрицательным.
Абсциссу точки В обозначим хB, ординату обозначим yB

| • Синусом называется отношение • Косинусом называется отношение • Тангенс определяется как • Котангенс определяется как • Секанс определяется как • Косеканс определяется как |
Чётность функций
Дата добавления: 2016-06-24; просмотров: 1834;
