Вынужденные колебания точки в отсутствие сопротивления среды

Пусть на точку М действуют две силы:

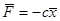- восстанавливающая;

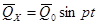- возмущающая гармоническая сила, где p – частота возмущающей силы.

Колебания, происходящие под действием возмущающей силы, называются вынужденными.

Дифференциальное уравнение движения точки М имеет вид:

.

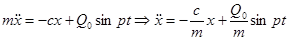Обозначим: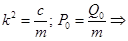

.

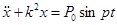Это линейное неоднородное дифференциальное уравнение второго порядка, решение которого имеет вид [1]:

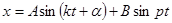
Собственные вынужденные

Колебания

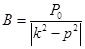- амплитуда вынужденных колебаний не зависит от начальных условий. Подбирая соотношения частот собственных и вынужденных колебаний можно получать вынужденные колебания с различными амплитудами В.

.

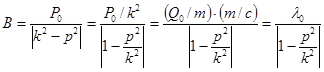где 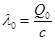- величина статического отклонения точки под действием силы .

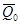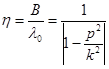- коэффициент динамичности, показывает во сколько раз амплитуда В вынужденных колебаний больше статического отклонения 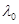. Коэффициент динамичности 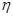зависит от отношения частот вынужденных p и собственных k колебаний:

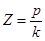- коэффициент расстройства.

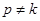Если , то есть 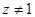, то вынужденные колебания точки в среде без сопротивления являются гармоническими колебаниями с постоянной амплитудой. Их частота совпадает с частотой возмущающей силы 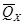. Они совершенно не зависят от начальных условий. Если 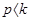, то фаза вынужденных колебаний совпадает с фазой возмущающей силы. Если 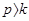, то фазы противоположны.

Если 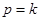, то есть z=1, частоты собственных и вынужденных колебаний совпадают, имеет место явление резонанса. В этом случае амплитуда колебаний со временем неограниченно возрастает. Практически этот случай невозможен, так как сопротивление хотя бы очень малое присутствует.