Затухающие колебания точки при линейном законе сопротивления среды
 Пусть на точку М при ее движении действуют две силы:
Пусть на точку М при ее движении действуют две силы:
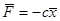 - восстанавливающая;
- восстанавливающая;
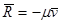 - сила вязкого трения (сопротивления), направленная против движения, μ - коэффициент сопротивления.
- сила вязкого трения (сопротивления), направленная против движения, μ - коэффициент сопротивления.
Дифференциальное уравнение движение точки:
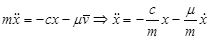 .
.
Обозначим: 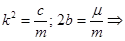
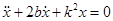 .
.
Это дифференциальное уравнение свободных колебаний точки при сопротивлении среды пропорциональном ее скорости движения. Его решение имеет вид [1]:
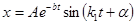 ,
,
где 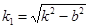 ; при
; при 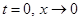
Это закон затухающих колебаний.
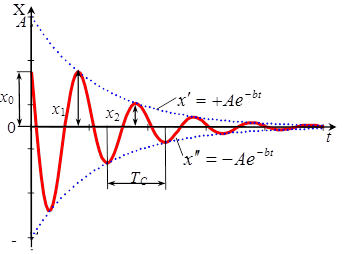
Свойства затухающих колебаний:
ü график затухающих колебаний заключен между кривыми 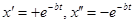 , так как
, так как 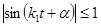 ;
;
ü период затухающих колебаний 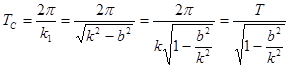 .
.
ü если 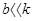 , то
, то 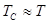 , то есть очень малое сопротивление на период затухающих колебаний не влияет, происходит постепенное затухание колебаний за счет уменьшения амплитуды колебаний по закону геометрической прогрессии со знаменателем
, то есть очень малое сопротивление на период затухающих колебаний не влияет, происходит постепенное затухание колебаний за счет уменьшения амплитуды колебаний по закону геометрической прогрессии со знаменателем 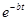 ;
;
ü быстрота затухания колебаний характеризуется логарифмическим декрементом затухания колебаний – логарифмом отношения двух смежных амплитуд:
ü 
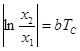 ;
;
ü если 
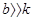 , то есть сопротивление очень велико, движение не будет колебательным, это так называемое апериодическое движение;
, то есть сопротивление очень велико, движение не будет колебательным, это так называемое апериодическое движение;
ü при 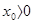 график апериодического
график апериодического  движения имеет вид изображенный на рисунке, при
движения имеет вид изображенный на рисунке, при 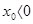 графики симметричны относительно оси t;
графики симметричны относительно оси t;
ü если 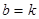 , то движение также апериодическое, а графики аналогичны.
, то движение также апериодическое, а графики аналогичны.
Вопросы для самоконтроля
Ø Какая сила вызывает гармонические колебания точки по прямой?
Ø Что называют амплитудой, фазой, начальной фазой, периодом и частотой колебаний? Какие из этих параметров зависят от начальных условий?
Ø Как определяется статическое отклонение центра гармонических колебаний?
Ø Как определяется жесткость эквивалентной пружины при различных способах соединения пружин?
Ø Под действием каких сил материальная точка совершает затухающие колебания. Перечислите свойства затухающих колебаний точки.
ЛЕКЦИЯ №11
Дата добавления: 2016-05-11; просмотров: 1505;
