Гармонические колебания точки под действием восстанавливающей силы
 Рассмотрим колебания точки по прямой ОХ.
Рассмотрим колебания точки по прямой ОХ.
Пусть точка М движется под действием одной силы 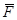 , которая всегда направлена по прямой к неподвижному центру О и пропорциональна расстоянию до этого центра, то есть
, которая всегда направлена по прямой к неподвижному центру О и пропорциональна расстоянию до этого центра, то есть 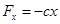 . Эту силу называют восстанавливающей.
. Эту силу называют восстанавливающей.
Пример восстанавливающей силы – сила упругости, тогда с – коэффициент упругости,
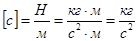 .
.
Уравнение движения точки М:
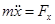 или
или 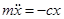 .
.
Обозначим 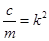 , тогда
, тогда
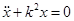 - уравнение свободных гармонических колебаний точки М в отсутствие сопротивление среды. Это - дифференциальное линейное однородное уравнение второго порядка, решение которого определяет закон свободных гармонических колебаний [1]:
- уравнение свободных гармонических колебаний точки М в отсутствие сопротивление среды. Это - дифференциальное линейное однородное уравнение второго порядка, решение которого определяет закон свободных гармонических колебаний [1]:
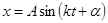 ,
,
где A – амплитуда колебаний – максимальное отклонение точки М от точки О – центра колебаний, [А]=1м;
α – начальная фаза колебаний, [α] = 1рад.;
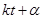 - фаза колебаний;
- фаза колебаний;
k - круговая частота колебаний, [k]=1рад/с.
Промежуток времени, в течение которого точка М совершает одно полное колебание, называется периодом колебаний Т.
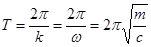 .
.
Найдем значения А и α. Начальные условия:
при 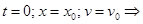
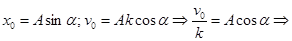

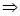
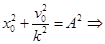
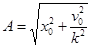 .
.
Поделив 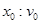 ,получим
,получим
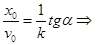
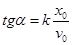
Из полученных выражений следует, что амплитуда колебаний А и начальная фаза α зависят от начальных условий 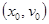 .
.
Свойства свободных гармонических колебаний:
ü  график движения точки, совершающей гармонические колебания, имеет вид
график движения точки, совершающей гармонические колебания, имеет вид  :
:
ü  амплитуда А и начальная фаза α зависят от начальных условий;
амплитуда А и начальная фаза α зависят от начальных условий;
ü частота колебаний k (период Т)от начальных условий не зависят, это характеристики данной колебательной системы (например, зависят от жесткости пружины с);
ü если помимо восстанавливающей силы 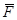 на точку действует постоянная сила
на точку действует постоянная сила 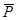 , то сила
, то сила 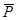 не изменяет характер колебаний, но смещает центр колебаний в сторону действия этой силы на величину статического отклонения
не изменяет характер колебаний, но смещает центр колебаний в сторону действия этой силы на величину статического отклонения
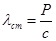 , откуда период таких колебаний равен
, откуда период таких колебаний равен
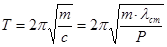 .
.
При решении задач встречаются случаи, когда колебательная система состоит из нескольких упругих элементов соединенных тем или иным способом. При этом жесткость эквивалентной пружины определяются следующим образом:
а) b) c)

a) параллельное соединение упругих элементов
с = с1+ с2;
b) последовательное соединение упругих элементов
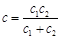 ;
;
c) груз размещен между упругими элементами
с = с1+ с2.
Дата добавления: 2016-05-11; просмотров: 1131;
