Принципы относительности
Напомним, что основной закон динамики (второй закон Ньютона) выполняется только в инерциальных системах отсчета.
Только для инерциальных систем отсчета выполняется принцип относительности Галилея: Все механические явления в инерциальных системах отсчета протекают одинаково, то есть никакими опытами нельзя обнаружить инерциальное движение системы отсчета, участвуя в движении вместе с ней.
Принцип относительности Эйнштейна: Все физические явления во всех инерциальных системах отсчета протекают одинаково.
12.1.2 Динамическая теорема Кориолиса.
Пусть точка М под действием приложенных к ней сил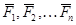 
движется по отношению к осям XOYZ. Эти оси движутся по отношению к инерциальной системе отсчета (например, неподвижным осям) 
.
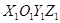По теореме Кориолиса абсолютное ускорение точки М равно:
.
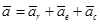Основной закон динами для точки М:
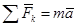
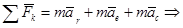
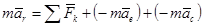Обозначим:
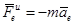- переносная сила инерции;
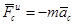- кориолисова сила инерции.
.
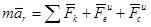Это основной закон динамики для относительного движения точки (общий случай) - динамическая теорема Кориолиса: Материальная точка движется относительно неинерциальной системы отсчета также как относительно инерциальной, только к действующим силам надо прибавить переносную и кориолисову силу инерции.
Частные случаи:
ü Подвижные оси XOYZ движутся поступательно. Угловая скорость подвижных осей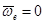 
.
.
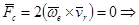
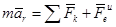ü Подвижные оси XOYZ движутся поступательно равномерно и прямолинейно. ,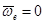 
.
.
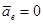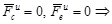
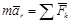В этом случае закон относительного движения аналогичен абсолютному движению.
Следствие: Система отсчета, движущаяся поступательно равномерно и прямолинейно, является инерциальной. В ней выполняются принципы относительности Галилея и Эйнштейна.
ü Точка М покоится по отношению к подвижным осям: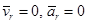 
.
.
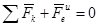Это уравнение относительного равновесия (покоя) точки (тела). То есть уравнения относительного равновесия составляют также как уравнения равновесия в неподвижных осях, но при этом к действующим на точку (тело) силам прибавляют переносную силу инерции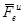 
.
Дата добавления: 2016-05-11; просмотров: 597;