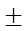Масса системы. Центр масс
Движение систем зависит не только от действующих на нее сил, но и от ее суммарной массы 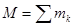 и ее распределения в системе. Распределение массы в системе характеризуется:
и ее распределения в системе. Распределение массы в системе характеризуется:
Ø координатами центра масс;
Ø осевыми моментами инерции;
Ø центробежными моментами инерции;
Ø моментами инерции относительно плоскости.
Точка С, координаты которой определяются следующими выражениями, называется центром масс (центром инерции):
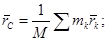
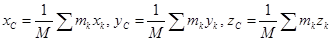
12.2.3 Моментом инерции точки К относительно оси Z называют положительную величину 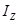 равную произведению массы точки
равную произведению массы точки 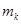 на квадрат ее расстояния до оси
на квадрат ее расстояния до оси 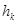 :
:
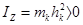 ,
, 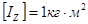 .
.
Моментом инерции механической системы (тела) относительно оси Z (осевым моментом инерции) называется положительная величина равная сумме моментов инерции всех ее точек относительно этой оси:
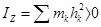 .
.
 Осевой момент инерции является мерой инертности тела при вращательном движении, поэтому его называют вращательной массой.
Осевой момент инерции является мерой инертности тела при вращательном движении, поэтому его называют вращательной массой.
В декартовой системе координат
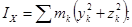
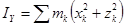 ;
;
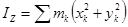
В случае сплошной среды
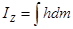 .
.
Вводят характеристику, не зависящую от формы тела, - радиус инерции ρ. Радиус инерции - это расстояние от оси Z до такой точки, в которую следует поместить всю массу тела M, чтобы момент инерции этой точки равнялся моменту инерции тела относительно этой оси.
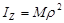 .
.
 12.2.3 Моменты инерции некоторых однородных тел:
12.2.3 Моменты инерции некоторых однородных тел:
Момент инерции тонкого однородного стержня длиной l, массой m относительно оси Z перпендикулярной ему и проходящей через центр масс 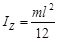 . .
| |||
Момент инерции тонкого однородного стержня длиной l, массой m относительно оси Z перпендикулярной ему и проходящей через центр масс 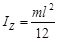 . .
| 
| ||
Момент инерции сплошного однородного диска (сплошного цилиндра) относительно его оси симметрии 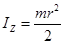 . .
| 
| ||
Момент инерции тонкого однородного кольца (полого цилиндра) относительно оси симметрии 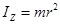
| 
| ||
Момент инерции прямоугольной сплошной тонкой пластины
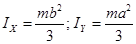
| 
| ||
Момент инерции сплошного конуса (круглого) относительно оси симметрии 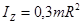 . .
| 
| ||
Момент инерции сплошного шара относительно оси проходящей через его центр 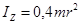 . .
|  
| ||
Момент инерции однородного кольца относительно оси проходящей через его центр в плоскости кольца
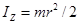
| 
| ||
Момент инерции сплошного однородного диска относительно оси проходящей через его центр в плоскости диска
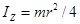
|
|
 12.2.4 Теорема Гюйгенса: Момент инерции тела относительно данной оси OZ равен моменту инерции относительной оси ей параллельной и проходящей через центр масс CZ' плюс произведение массы тела на квадрат расстояния между осями.
12.2.4 Теорема Гюйгенса: Момент инерции тела относительно данной оси OZ равен моменту инерции относительной оси ей параллельной и проходящей через центр масс CZ' плюс произведение массы тела на квадрат расстояния между осями.
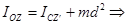
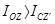 -момент инерции тела относительно оси проходящей через центр масс всегда наименьший.
-момент инерции тела относительно оси проходящей через центр масс всегда наименьший.
 12.2.5 Центробежные моменты инерции равны:
12.2.5 Центробежные моменты инерции равны:
|

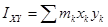 ;
;
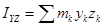 ;
;
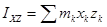 .
.
Дата добавления: 2016-05-11; просмотров: 786;