В колебательном контуре

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические вели-чины (заряды, токи) периодически изменя­ю-тся и которые сопровождаются взаимными превращениями электрического и магнит­ного полей.

Для возбуждения и поддержания электро-магнитных колебаний использует­ся колеба-тельный контур - цепь, состоящая из вклю-ченных последовательно катушки индуктив-нос-тью L, конденсатора емкостью С и резис-тора сопротивлением R.

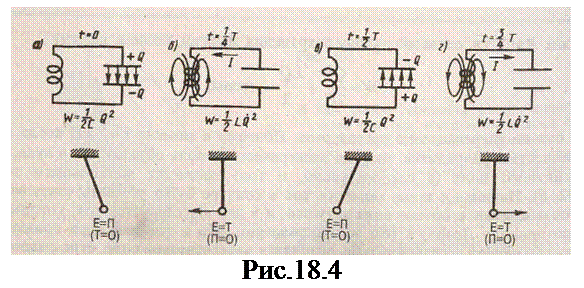Рассмотрим последовательные стадии колебательного процесса в идеализирован­ном контуре, сопротивление которого пренебре-жимо мало (R»0) (рис.18.4). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Тогда в начальный момент времени t=0 (рис.18.4,а)между обкладками конденсатора возникнет электри-ческое поле, энергия которого 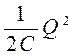(энергия плоского заряженного конденсатора). Если замкнуть конденсатор на катушку индуктив-ности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (она равна ¹/₂ LQ²) — воз­растать.

Так как R»0,то, согласно закону сохране-ния энергии, полная энергия

,

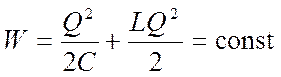так как она на нагревание не расходуется. Поэтому в момент t = ¹/₄T, когда конденсатор полностью разрядится, энергия электричес-кого поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения (рис.18.4, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцирует-ся ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис.18.4, в). Далее те же процессы начнут протекать в обратном направлениии система к моменту времени t = Т придет в перво-начальное состояние (рис.18.4, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей.

Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис.18.4, внизу), сопровождающимися взаимными превраще-ниями потенциальной и кинетической энер-гий маятника. В данном случае энергия электрического поля конденсатора (Q²/(2C))аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ²/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник.

Согласно закону Ома, для контура, содер-жащего катушку индуктивностью L конден-сатор емкостью С и резистор сопротивлением R, '

,

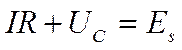где IR — напряжение на резисторе, U_С=Q/C — напряжение на конденсаторе, 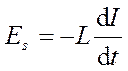- э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока ( Е_s — единственная э.д.с. в контуре). Следовательно,

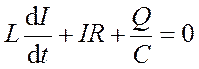. (18.25)

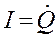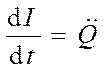Разделив (18.25) на L и подставив и ,получим дифференциальное уравне-ние колебаний заряда Q в контуре:

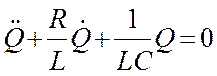. (18.26)

В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гарманическими. Тогда из (18.26) получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре:

.

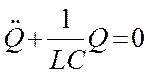Из выражений(18.16) и (18.1) вытекает, что заряд Q совершает гармонические колеба-ния по закону

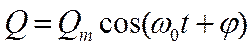, (18.27)

где Q_m - амплитуда колебаний заряда конден-сатора с циклической (угловой) частотой w₀, называемой собственной частотой контура

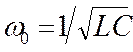,(18.28)

и периодом

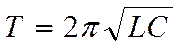. (18.29)

формула (18.29) впервые была получена У. Томсоном и называется формулой Томсона.

Сила тока в колебательном контуре

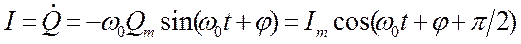, (18.30)

где I_m=w₀Q_m - амплитуда силы тока.

Напряжение на конденсаторе

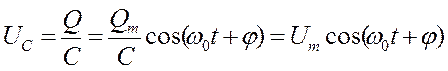, (18.31)

где U_m= Q_m/C — амплитуда напряжения.

Из выражений (18.27) и (18.30) вытекает, что колебания тока I опережают по фазе колебания заряда Q на p/2, т.е., когда ток достигает максимального значения, заряд (а также и напряжение (см. (18.31)) обращается в нуль, и наоборот.