Механические гармонические колебания
Механические и электромагнитные колебания
Гармонические колебания и их
Характеристики
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колеба-тельные процессы широко распространены в природе и технике, например качание маят-ника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напря-жение и ток в цепи. Физическая природа коле-баний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процес-сы описываются одинаковыми характеристи-ками и одинаковыми уравнениями. Отсюда следует целесообразность единого подходак изучению колебаний различной физической природы.Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д.У. Рэлеем (1842—1919), А.Г. Столетовым, русским инженером-экспериментатором П.Н. Лебедевым (1866—1912). Большой вклад в развитие теории колебаний внесли Л.И. Мандельштам (1879—1944) и его ученики.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздейст-вий на колебательную систему (систему, совершающую колебания). Простейшим ти-пом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам:
1) колебания, встречающиеся природе и технике, часто имеют характер, близкий к гармоническому;
2) различные периодические процессы (процессы, повторяющиеся через равные про-межутки времени) можнопредставить как наложение гармонических колебаний. Гармо-нические колебания величины s описываются уравнением типа
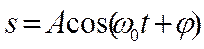,(18.1)
где А - максимальное значение колеблю-щейся величины, называемое амплитудой колебаний, w0 - круговая (циклическая) частота, j - начальная фаза колебания в мо-мент времени t=0, (w0t+j) - фаза колебания в момент времени t.
Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до –А.
Промежуток времени Т через который повторяются определенные состояния систе-мы, совершающей гармонические колебания называется периодом колебания. За период колебаний фаза колебания получает приращение 2p, т.е.
w0 (t+Т)=(w0t+j)+2p,
откуда
Т=2p/w0. (18.2)
Величина, обратная периоду колебаний,
n=1/Т, (18.3)
т.е. число полных колебаний, совершаемых в единицу времени, называется частотой коле-баний. Сравнивая (18.2) и (18.3), получим выражение для круговой (угловой) частоты
w0=2pn.
Единица частоты — герц (Гц): 1 Гц - частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
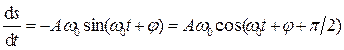;(18.4)
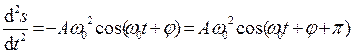,(18.5)
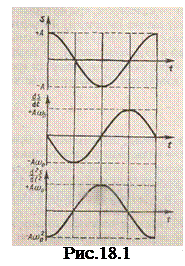т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (18.4) и (18.5) соответственно равны Аw0 и Аw02. Фаза величины (18.4) отличается от фазы величины (18.1) на p/2, а фаза величины (18.5) отличается от фазы величины (18.1) на p. Следовательно, в моменты времени, когда s=0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d2s/dt2 приобретает наибольшее положительное значение (рис.18.1).
Из выражения (18.5) следует дифференциальное уравнение гармонических колебаний
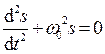,(18.6)
(где s=Acos(w0t+j)). Решением этого уравнения является выражение (18.1).
Изображение гармонических колебаний с помощью вращающегося вектора амплитуды.
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаг-рамм. Для этого из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладываетсявектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис.18.2).
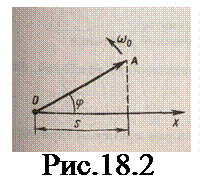Если этот вектор привести во вращение с угловой скорос-тью w0, равной циклической (угловой) частоте колебаний, то проекция конца вектора будет перемещаться по оси x b принимать значения от -А до +А, а колеблю-щаяся величина будет изменяться со временем по закону s=Acos(w0t+j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбран-ную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью w0t вокруг этой точки.
В физике часто применяется другой метод, который отличается от метода вращающегося вектора амплитуды лишь по форме. В этом методе колеблющуюся величину представля-ют комплексным числом. Согласно формуле Эйлера, для комплексных чисел
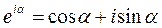, (18.7)
где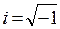 
- мнимая единица. Поэтому уравнение гармонического колебания (18.1) можно записать в комплексной форме:
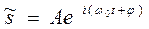(18.8)
Вещественная часть выражения (18.8)
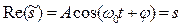
представляет собой гармоническое колебание. Обозначение Re вещественной части условимся опускать и (18.8) будем записывать в виде
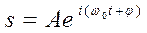
В теории колебаний принимается, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
Механические гармонические колебания
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (18.1), где s=x:
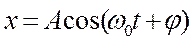. (18.9)
Согласно выражениям (18.4) и (18.5), ско-рость n и ускорение аколеблющейся точки соответственно равны
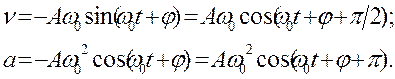(18.10)
Сила F=ma, действующая на колеблющу-юся материальную точку массой т с (18.9) и (18.10) равна
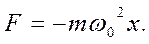
Следовательно, сила пропорциональна сме-щению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия)
Кинетическая энергия материальной точки, совершающей прямолинейные гармо-нические колебания, равна
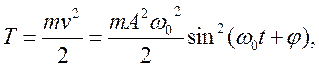(18.11)
или
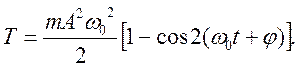. (18.12)
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна
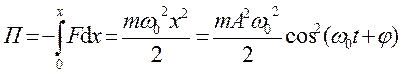, (18.13)
или
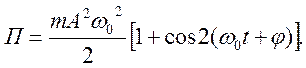(18.14)
Сложив (18.11) и (18.13), получим формулу для полной энергии:
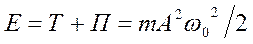. (18.15)
Полная энергия остается постоянной, так как при гармонических колебаниях справед-лив закон сохранения механической энергии, поскольку упругая сила консервативна.
18.3. Гармонический осциллятор. Пружин-
Дата добавления: 2016-06-24; просмотров: 2681;