Взаимное расположение прямых на эпюре.
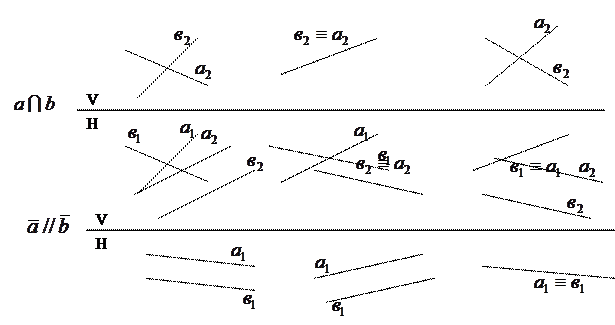 | |||
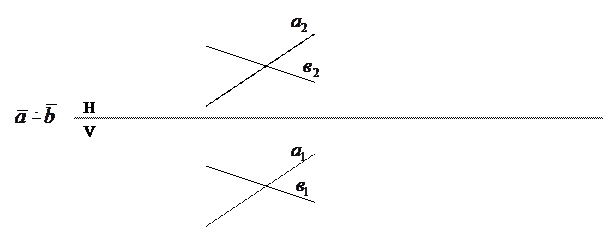 |
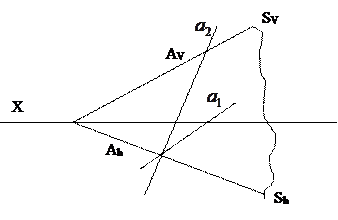
Утверждения
1. 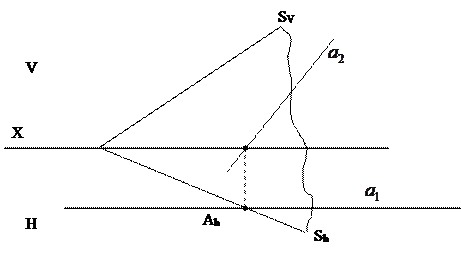 Прямая а1, заданная горизонтальной и вертикальной проекцией не параллельной плоскости проектирования, лежит в плоскости соответственно плоскости α .
Прямая а1, заданная горизонтальной и вертикальной проекцией не параллельной плоскости проектирования, лежит в плоскости соответственно плоскости α .
2. Прямая а(а1,а2) параллельна плоскости V лежит в плоскости α(SV,Sh)  , когда след Аh
, когда след Аh 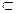 Sh, а1 параллельна оси проекции, а2 параллельна Sh.
Sh, а1 параллельна оси проекции, а2 параллельна Sh.
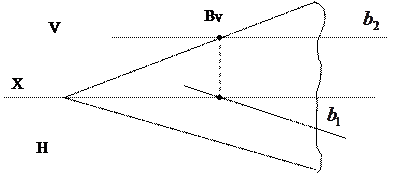
3. Прямая b1 , задання проекциями b1, b2 , параллельна плоскости h, лежит в плоскости α(SV,Sh)  , когда след br
, когда след br 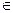 Sr в b2 параллельной оси проектных b1 параллельна Sh.
Sr в b2 параллельной оси проектных b1 параллельна Sh.
Определение 11.1. Изображение некоторой фигуры F называется полным, если к нему можно присоединить изображение некоторого аффинного репера, так что все точки и прямые фигуры F будут определяться. В противном случае – изображение неполное.
К полным изображениям относятся изображения призмы, цилиндра, конуса, шара.
полная фигура  Шестивершинник
Шестивершинник  изображение
изображение
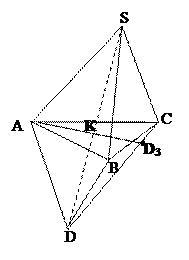 неполное
неполное
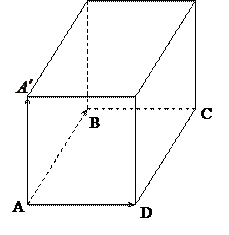 | |||
| |||
Замечание: Если необходимо построить сечение плоскости некоторой фигуры, где её изображение является неполным, то можно дополнить его до полного произвольным введением элементов.
Задача: Дано изображение пирамиды DABC и прямая пересечения её грани АВD и BCD в точках M и N соответственно. Найти след прямой MN на плоскости основания основание АВС.

 Задача:
Задача:
Построить точку Х (аксонометрическую проекцию) по заданной вторичной проекции Х3 , если известно, что точка Х пространства лежит в плоскости заданной тремя точками (АА3), (ВВ3), (СС3).
1. В3С3
2. А3Х3
3. А3Х3 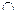 В3С3
В3С3
4. АА3 //LL3
5. BC 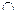 LL3= L
LL3= L
6. AL
7. XX3 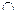 AL=X
AL=X
Задача:
Построить след плоскости, заданной тремя точками, не лежащими на одной прямой (АА3, ВВ3, СС3 ).
1.А0=АВ 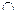 А3В3
А3В3
2. В0=ВС 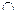 В3С3
В3С3
. С0=АС 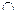 А3С3
А3С3
 P0 =А0В0 –искомая.
P0 =А0В0 –искомая.
Дата добавления: 2017-01-29; просмотров: 815;

 D3
D3