Теоремы о пределах.
Теорема 1. Наличие предела последовательности и его конкретное значение не зависит от любого конечного числа членов последовательности (из последовательности можно удалить любое конечное количество членов последовательности).
Теорема 2. Если у последовательности существует предел, то он единственный.
Доказательство: «от противного»
Предположим. Что последовательность имеет два предела, причем один больше другого, т.е. an→a; an →b, причем b>a; тогда изобразим эпсилон-окрестность чисел a и b (Oe (a) и Oe (b)), если 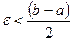
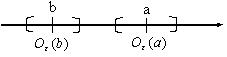 В этом случае эпсилон-окрестности не пересекаются. Тогда начиная с некоторого номера все члены последовательности должны оказаться одновременно и в Oe (a) и в Oe (b), что невозможно, т.к. они не пересекаются Þ двух разных значений предела быть не может.
В этом случае эпсилон-окрестности не пересекаются. Тогда начиная с некоторого номера все члены последовательности должны оказаться одновременно и в Oe (a) и в Oe (b), что невозможно, т.к. они не пересекаются Þ двух разных значений предела быть не может.
Теорема 3. «О пределе суммы, произведения и частного»
Если последовательность an имеет предел а, последовательность bn имеет предел b, то последовательность:
§ an ± bn → a ± b
§ an × bn → a × b
§ 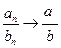 , если b ≠ 0, bn ≠ 0
, если b ≠ 0, bn ≠ 0
Доказательство:
1) убедимся, что разница (an ± bn) – (a ± b) является бесконечно малой величиной.
an = a + αn , αn → 0; bn = b + βn , βn → 0; подставим эти выражения в разность:
(a + αn) ± (b + βn) – (a ± b) = (αn ± βn) это выражение →0 Þ является бесконечно малой величиной. Ч.т.д.
2) αnbn – ab: an = a + αn , αn → 0; bn = b + βn , βn → 0; подставим эти выражения в разность: (a + αn) (b + βn) – ab = ab +bαn + aβn + αnbn – ab = bαn + aβn + αnbn каждое слагаемое этой суммы является бесконечно малой величиной Þ теорема доказана.
3) убедимся в том, что разница 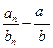 является бесконечно малой величиной. Как только это выяснится, третья часть Теоремы будет доказана.
является бесконечно малой величиной. Как только это выяснится, третья часть Теоремы будет доказана.
Т.к. a и b – это пределы Þ последовательности an и bn могут быть представлены в виде: an = a + αn , αn → 0; bn = b + βn , βn → 0; подставим эти выражения в разность:
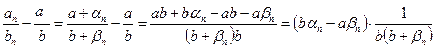
величина 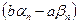 является бесконечно малой, а величина
является бесконечно малой, а величина 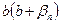 начиная с некоторого номера будет
начиная с некоторого номера будет 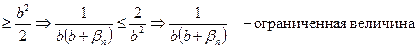
Произведение бесконечно малой величины на ограниченную является бесконечно малой величиной Þ разность 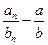 является бесконечно малой величиной Þ теорема доказана.
является бесконечно малой величиной Þ теорема доказана.
Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется пределом функции f(x) при x®a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.
Определение 2. Постоянное число А называется пределом функции f(x) при x®a, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 < ½x-a½ < d, значения функции f(x) будут лежать в e-окрестности числа А, т.е. êf(x)-A ê < e.
Это определение называют определением предела функции по Коши, или “на языке e - d“.
Определения 1 и 2 равносильны. Если функция f(x) при x ® a имеет предел, равный А, это записывается в виде 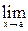 f(x) = A.
f(x) = A.
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде: 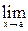 f(x) = ¥ (
f(x) = ¥ ( 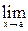 f(x) = - ¥).
f(x) = - ¥).
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной.
Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
Для нахождения пределов на практике пользуются следующими теоремами.
Пусть функция 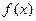 определена на некотором промежутке
определена на некотором промежутке 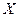 и пусть точка
и пусть точка 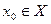 или
или 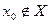
Определение 1. Число А называется пределом функции 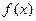 в точке
в точке 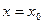 , если для любого числа
, если для любого числа 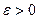 существует число
существует число 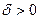 такое, что для всех
такое, что для всех 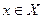 ,
, 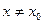 , удовлетворяющих неравенству
, удовлетворяющих неравенству 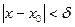 , выполняется неравенство
, выполняется неравенство 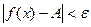 .
.
Можно сформулировать несколько иначе:
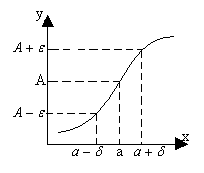
Определение: пусть имеется функция f (x), которая определена в некоторой окрестности точки а, но может быть не определена в самой точке а, тогда пределом функции f (x) при x → a называют число А, такое, что для любого сколь угодно малого e > 0 найдется положительное число δ > 0, такое, что как только х попадает в эпсилон-окрестность числа а (Oδ (а)), так сразу f (x) попадает в Oe (А), т.е.: 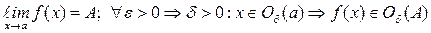
Пример 1. Используя определение, доказать, что функция 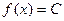 (С – некоторое число) в точке
(С – некоторое число) в точке 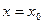 (
( 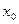 - любое число) имеет предел, равный С, т.е.
- любое число) имеет предел, равный С, т.е. 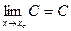
Решение. Возьмем любое 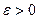 . Тогда для любого
. Тогда для любого 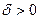 числа выполняется требуемое неравенство
числа выполняется требуемое неравенство 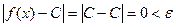 ; следовательно,
; следовательно, 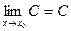 .
.
Пример 2. Используя определение, доказать, функция 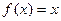 в точке
в точке 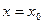 имеет предел, равный, т.е.
имеет предел, равный, т.е. 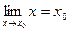
Решение. Возьмем любое 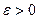 . Тогда для всех
. Тогда для всех 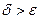 , удовлетворяющих неравенству
, удовлетворяющих неравенству 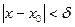 , выполняется требуемое неравенство
, выполняется требуемое неравенство 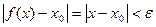 ; следовательно,
; следовательно, 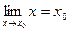 .
.
Пример 3. Используя определение, доказать, функция 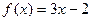 в точке x=1 имеет предел, равный единице т.е.
в точке x=1 имеет предел, равный единице т.е. 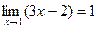 .
.
Решение. Возьмем любое 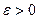 . Задача состоит в том, чтобы по этому
. Задача состоит в том, чтобы по этому 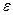 найти такое
найти такое 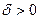 , при котором из неравенства
, при котором из неравенства 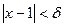 следовало бы неравенство
следовало бы неравенство 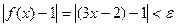 . Преобразуя последнее неравенство, получаем
. Преобразуя последнее неравенство, получаем 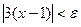 , или
, или 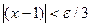 . Отсюда видно, что если взять
. Отсюда видно, что если взять 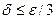 , то для всех x, удовлетворяющих неравенству
, то для всех x, удовлетворяющих неравенству 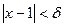 , выполняется требуемое неравенство
, выполняется требуемое неравенство 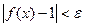 . Это и означает, что
. Это и означает, что 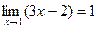 .
.
Свойства пределов
Пусть функции 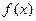 и
и 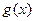 имеют в точке
имеют в точке 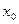 пределы A и B. Тогда
пределы A и B. Тогда
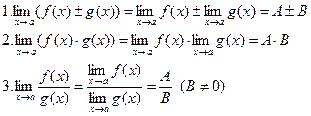
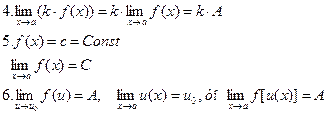
Замечание. Эти равенства верны и в случае, когда a является одним из символов 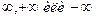 . Теорема 1. Если существуют пределы
. Теорема 1. Если существуют пределы 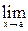 f(x)=A,
f(x)=A, 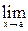 g(x)=B, то
g(x)=B, то
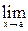 (f(x)+(g(x)) = A + B,
(f(x)+(g(x)) = A + B, 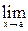 f(x) g(x) = AB,
f(x) g(x) = AB, 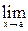 f(x)/g(x) = A/B (B ¹ 0).
f(x)/g(x) = A/B (B ¹ 0).
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”.
Теорема 2. 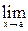 (f(x))a = (
(f(x))a = ( 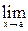 f(x)) a, где a = const, т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,
f(x)) a, где a = const, т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, 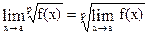 ;
;
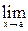 bf(x) =bA, где b = const,
bf(x) =bA, где b = const, 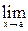 f(x)=A;
f(x)=A; 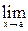 logc f(x) = logc
logc f(x) = logc 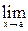 f(x), где c = const.
f(x), где c = const.
Теорема 3. 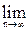
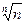 = 1,
= 1, 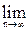
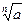 = 1,
= 1,
Дата добавления: 2016-06-24; просмотров: 1122;
