Прямая в пространстве. Прямая и плоскость
Различным способам задания прямой в пространстве соответствуют разные виды ее уравнений, основные из которых представлены в таблице. Таблица
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
Канонические уравнения прямой
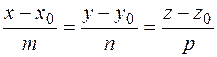
| (x0,y0,z0) – координаты точки М0, лежащей на прямой; m,n,p – координаты вектора, параллельного прямой | Вектор 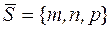 называется направля-ющим вектором прямой называется направля-ющим вектором прямой
| |
Уравнение прямой, проходящей через две заданные точки
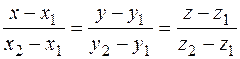
| (x1,y1,z1), (x2,y2,z2) – координаты двух заданных точек | Уравнение является обобще-нием уравнения прямой на плоскости | |
Уравнения прямой как линии пересечения двух плоскостей
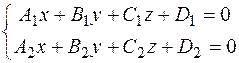
| 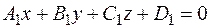 - уравнение одной плоскости; - уравнение одной плоскости;
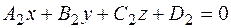 - уравнение второй плоскости - уравнение второй плоскости
| Уравнение иначе назы-вается общими уравне-ниями прямой в простран-стве |
Пусть заданы две прямые своими каноническими уравнениями:
l1: 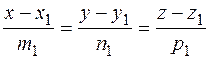
l2: 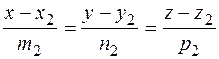 .
.
Угол между прямыми определяется как 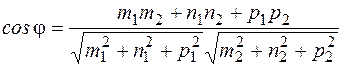 .
.
Условие перпендикулярности прямых:
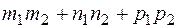 =0.
=0.
Условие параллельности прямых:
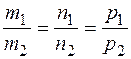 .
.
Пусть плоскость a задана уравнением Ах+Ву+Сz+D=0, а прямая l – своими каноническими уравнениями 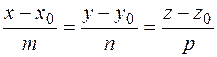 , тогда угол между прямой и плоскостью определяется как
, тогда угол между прямой и плоскостью определяется как
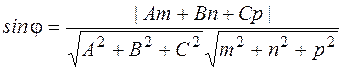 .
.
Условие параллельности прямой и плоскости Аm+Bn+Cp=0.
Условие перпендикулярности прямой и плоскости:
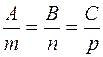 .
.
Дата добавления: 2016-06-24; просмотров: 551;
