Лекция 7 Теория пределов и непрерывности функции
(Тема 3.1.)
План лекции
Числовые последовательности, монотонные, ограниченные последовательности.
Предел последовательности, основные свойства предела.
Бесконечно малые и бесконечно большие величины, связь между ними.
Предел функции.
Свойства предела.
Замечательные пределы.
Односторонние пределы.
Понятие непрерывности функции.
Точки разрыва и их классификация.
Асимптоты графика функции.
Определение:Последовательностью называют упорядоченную переменную величину, у которой можно пронумеровать все значения, причем {xn}, n = 1, 2, 3, 4. . .
p<q, следовательно xp предыдущая к xq .
Примеры: 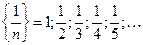 Гарм оническая последовательность.
Гарм оническая последовательность.
{0; 1111…1}=0,1; 0,11; 0,111;. . .; 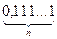
Предел последовательности
Постоянное число а называется пределом последовательности {xn} 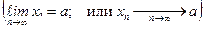 , если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенствуêxn - a ê < e.
, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенствуêxn - a ê < e.
Записывают это следующим образом: 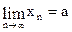 или xn ® a.
или xn ® a.
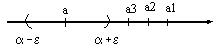 Неравенство равносильно двойному неравенству a- e < xn < a + e, которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Неравенство равносильно двойному неравенству a- e < xn < a + e, которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Т.о 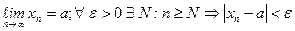
Точка а называется точкой сгущения.
Пример. Покажем, что пределом последовательности 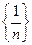 является 0.
является 0.
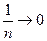 , выбираем ε. Путь дано ε >0, тогда решим неравенство:
, выбираем ε. Путь дано ε >0, тогда решим неравенство:
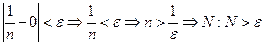 Начиная с
Начиная с 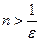 все члены последовательности <
все члены последовательности <
Определение:Последовательность называется бесконечно малой величиной, если её предел равен нулю.
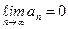 ;
; 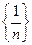 – бесконечно малая величина.
– бесконечно малая величина.
Для того чтобы число а являются пределом последовательности an необходимо и достаточно, чтобы члены этой последовательности были представлены в виде суммы предыдущих значений а и некоторые бесконечно малые величины n, т.е.
an = a + n, где 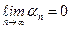
Дата добавления: 2016-06-24; просмотров: 858;
