Применение дифференциала для приближенных вычислений

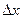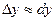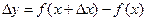
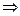
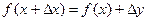
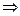
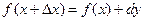Воспользуемся тем, что при достаточно малых приращение функции приближенно равно ее дифференциалу , а , или , .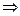

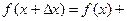
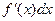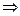
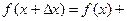
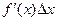Правила Лопиталя – Бернулли.

Пусть предел функции f (x) при х → а +0 равен нулю, т.е. 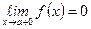, и пусть 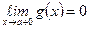, и пусть у функций f (x) и g (x) существует производная 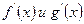во всех точках больших точки а, достаточно близких к а. Тогда, если существует предел отношения .

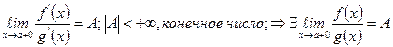Обратное утверждение неверно.

1. Неопределенность вида 0/0. Первое правило Лопиталя.

Если 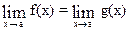= 0, то 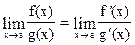, когда последний существует.

2. Неопределенность вида ¥/¥. Второе правило Лопиталя.

Если 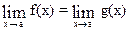= ¥, то 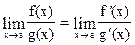, когда последний существует.

3. Неопределенности вида 0× ¥, ¥ - ¥, 1^¥ и 0⁰ сводятся к неопределенностям 0/0 и ¥/¥ путем алгебраических преобразований.

Исследование функций и построение графиков

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) £ f(x_о) (f(x) ³ f(x_о)).Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.Итак…

Определение. Функция 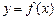имеет экстремум ( максимум или минимум ) в точке 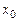, если 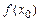является наибольшим или наименьшим значением функции в некоторой двусторонней окрестности этой точки.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ¢(x_о) = 0, либо f ¢(x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.Итак…

Необходимое условие существования экстремума. Функция 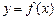имеет экстремум в точке 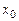, если первая производная функции 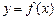в этой точке равна нулю 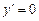или не существует. Первое достаточное условие. Пусть x_о - критическая точка. Если f ¢ (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.Второе достаточное условие. Пусть функция f(x) имеет производную
f ¢ (x) в окрестности точки x_о и вторую производную 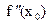в самой точке x_о. Если f ¢(x_о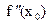) = 0, >0 ( 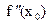<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же 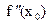=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.Итак…

Достаточные условия существования экстремума. Если функция 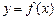непрерывна в точке 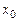и имеет в некоторой окрестности 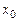кроме, может быть, самой точки 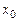, конечную производную и если при переходе через :

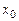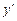· меняет свой знак с + на -, то точка 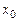- точка максимума ;

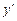· меняет свой знак с - на +, то точка 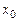- точка минимума ;

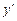· не меняет знака, то экстремума нет.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].