Схема исследования функции на выпуклость и вогнутость
1. Найти вторую производную функции 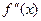 .
.
2. Найти точки, в которых 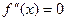 или не существует.
или не существует.
3. Нанести эти точки на числовую прямую и на каждом из полученных интервале определить знак второй производной 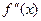 и сделать вывод об интервалах выпуклости и наличии точек перегиба.
и сделать вывод об интервалах выпуклости и наличии точек перегиба.
4. Найти значение функции в точках перегиба.
ПримерИсследовать функцию 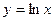 на выпуклость и вогнутость.
на выпуклость и вогнутость.
Решение: Область определения данной функции D(f)= 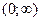 . Найдём производные первого и второго порядков:
. Найдём производные первого и второго порядков: 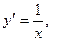
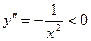 . Следовательно, функция
. Следовательно, функция 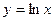 выпукла вверх на промежутке
выпукла вверх на промежутке 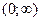 .Асимптоты графика функции.Пусть функция
.Асимптоты графика функции.Пусть функция 
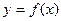 определена в некоторой окрестности точки
определена в некоторой окрестности точки 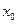 (исключая, возможно, саму эту точку). Прямая
(исключая, возможно, саму эту точку). Прямая 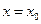 называется вертикальной асимптотой графика функции, если
называется вертикальной асимптотой графика функции, если 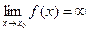 .
.
Замечание:Если прямая 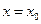 является вертикальной асимптотой графика функции, то точка
является вертикальной асимптотой графика функции, то точка 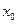 является точкой разрыва второго порядка и, следовательно, вертикальные асимптоты следует искать среди точек разрыва второго рода.
является точкой разрыва второго порядка и, следовательно, вертикальные асимптоты следует искать среди точек разрыва второго рода.
Прямая 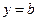 является горизонтальной асимптотой графика функции, если существует предел
является горизонтальной асимптотой графика функции, если существует предел 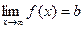 .
.
Прямая 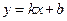 является наклонной асимптотой кривой
является наклонной асимптотой кривой 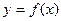 , если существуют пределы
, если существуют пределы 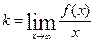 ,
, 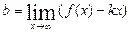 .
.
ПримерНайти все асимптоты уравнения 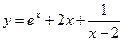 .
.
Решение: В точке x=2 функция неопределенна, значит это точка разрыва. Найдем в ней предел данной функции 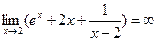 . Значит х=2 – вертикальная асимптота.
. Значит х=2 – вертикальная асимптота.
Проверим наличие горизонтальных асимптот: 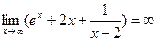 . Следовательно, горизонтальных асимптот нет.
. Следовательно, горизонтальных асимптот нет.
Проверим наличие наклонных асимптот: 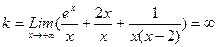 .Следовательно, наклонной асимптоты при
.Следовательно, наклонной асимптоты при 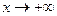 нет.
нет. 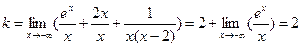 ,
, 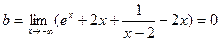 Значит
Значит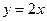 -уравнение наклонной асимптоты при
-уравнение наклонной асимптоты при 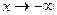 .
.
Дата добавления: 2016-06-24; просмотров: 970;
