ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Пусть функция определена и непрерывна на промежутке [a; b]. Для наглядности будем считать, что она неотрицательна.

Замечание: для введения понятия определенного интеграла требования непрерывности и неотрицательности не является обязательным.

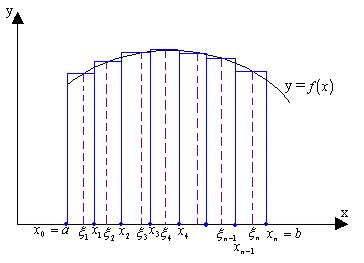
Разобьем промежуток [a; b] точками 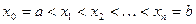на l отрезков .

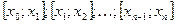Обозначим через 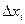длину отрезка номер i .

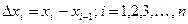На каждом отрезке выбираем точку .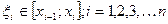

Точка 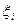на отрезке выбирается произвольно. После этого на каждом отрезке, как на основании, построим прямоугольник высотой .

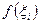Определение: интегральной суммой S_n называется следующая величина: .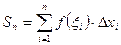

Если для функции выполнены условия неотрицательности и непрерывности, тот интегральная сумма S_n имеет смысл площади изображенной ступенчатой фигуры.

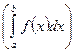Определение: определенным интегралом функции по промежутку [a; b] называется предел интегральных сумм, вычисленный при условии стремления к нулю длины наибольшего из отрезков на которые разбит промежуток [a; b], если этот предел существует независимо от способа разбиения отрезка [a; b] на мелкие отрезки и независимо от способа выбора точек ξ_i, т.е. .

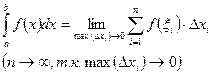Площадь ступенчатой фигуры при условии 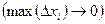будет стремиться к площади криволинейной трапеции под графиком . Поэтому можно сказать: геометрический смысл определенного интеграла состоит в том, что он равен площади криволинейной трапеции.

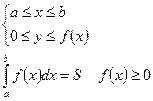
Если функция меняет знак на промежутке [a; b],тот определенный интеграл вычисляется следующим образом:

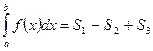
Определенный интеграл существует и от функций с разрывами. Можно доказать, что если функция имеет на промежутке [a; b] только разрывы первого рода и их счётное количество, то от этой функции существует определенный интеграл по промежутку [a; b].