Формула Ньютона – Лейбница.
Пусть функция  непрерывна при а ≥ х, тогда производная от определённого интеграла от функции
непрерывна при а ≥ х, тогда производная от определённого интеграла от функции  с переменным верхним пределом равна значению подынтегральной функции на верхнем пределе интегрирования, т.е.
с переменным верхним пределом равна значению подынтегральной функции на верхнем пределе интегрирования, т.е. 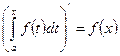 .
.
Доказательство:
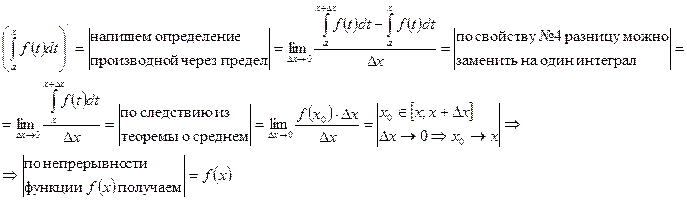
Из теоремы Барроу вытекает связь между определенным и неопределенным интегралами, а именно: определенный интеграл с переменным верхним пределом является одной из первообразных функции  . Обозначим эту первообразную через
. Обозначим эту первообразную через 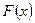 +с, где
+с, где 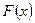 - это любая их первообразных
- это любая их первообразных  , а значение ‘с’ находится, т.е.
, а значение ‘с’ находится, т.е. 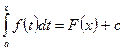 .
.
Запишем полученное равенство при х = а.
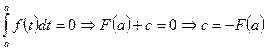 . Подставим полученное значение ‘c’ в формулу:
. Подставим полученное значение ‘c’ в формулу: 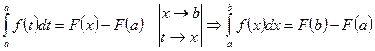 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.
Эту формулу часто пишут в таком виде: 
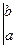 - символ подстановки (из верхнего предела отнимаем нижний).
- символ подстановки (из верхнего предела отнимаем нижний).
Пример: найти площадь между параболой у = 4 – х2 и осью Ох.

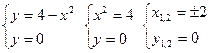
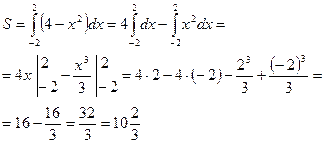
Формула интегрирования по частям для определённого интеграла.
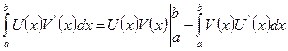
Сокращенная формула: 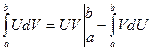
Пример: вычислить интеграл.
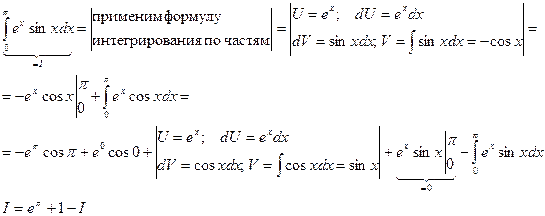
Мы получили уравнение, из которого можно найти интересующий нас интеграл: 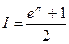
Дата добавления: 2016-06-24; просмотров: 1254;
