Несобственные интегралы.
Определение: несобственным интегралом с бесконечным верхним пределом интегрирования называется предел от определенного интеграла, вычисленный при условии стремления к бесконечности верхнего предела интегрирования, т.е. 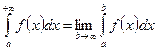 .
.
Если существует конечное значение данного предела, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Определение: аналогично вводятся несобственные интегралы с бесконечным нижним пределом интегрирования и с обоими бесконечными пределами интегрирования, а именно:
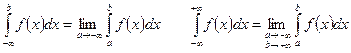 .
.
Замечание: несобственные интегралы с одним или двумя бесконечными пределами интегрирования называют также несобственными интегралами первого рода.
Пример:

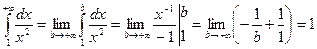
Мы получили, что площадь бесконечной фигуры равна 1. эту площадь надо понимать, как предел площадей конечных фигур, ограниченных вертикальными прямыми, когда правая граница фигуры стремится к бесконечности.
Вычисление несобственных интегралов вида: 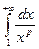
Замечание: в качестве нижнего предела интегрирования можно брать любое положительное число.
P > 1
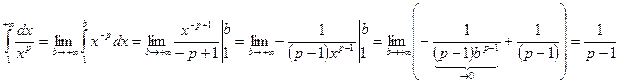 В этом случае (при p > 1) данный интеграл сходится.
В этом случае (при p > 1) данный интеграл сходится.
P < 1
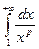 = все вычисления проводятся также, как в предыдущем пункте. После вычислений получаем:
= все вычисления проводятся также, как в предыдущем пункте. После вычислений получаем: 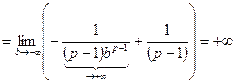
При p < 1 интеграл расходится.
3) p = 1
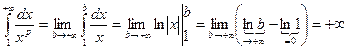
При p = 1 интеграл расходится.
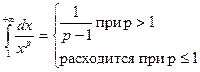
Дата добавления: 2016-06-24; просмотров: 1205;
