Свойства определенного интеграла.
1) 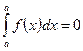 - это свойство считается по определению.
- это свойство считается по определению.
2) 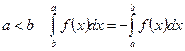 - по определению.
- по определению.
3)Определенный интеграл не зависит от обозначения переменной интегрирования, т.е. 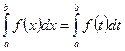 .
.
4) 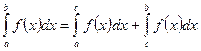 если эти интегралы существуют.
если эти интегралы существуют.
Доказательство:
1. Пусть a < c < b. Выберем разбиение отрезка [a; b] таким образом, чтобы точка с всегда попадала в это разбиение, тогда
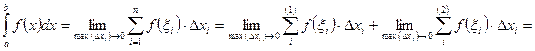
где: 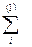 берется по всем промежуткам, находящимся левее точки с, а
берется по всем промежуткам, находящимся левее точки с, а 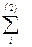 - по всем промежуткам, находящимся правее точки с
- по всем промежуткам, находящимся правее точки с
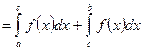
2. Пусть a < b < c
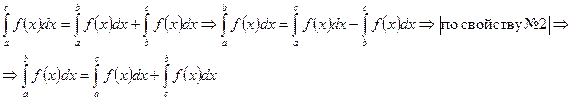
5)Определенный интеграл от суммы и разности функций равен соответственно сумме или разности интегралов этих функций, если они существуют, т.е.
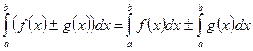 . Это свойство вытекает из того, что предел суммы или разности равен соответственно сумме или разности пределов.
. Это свойство вытекает из того, что предел суммы или разности равен соответственно сумме или разности пределов.
6)Постоянный множитель можно выносить за знак определенного интеграла.
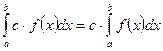 . Это свойство вытекает из того, что постоянный множитель можно выносить за знак предела.
. Это свойство вытекает из того, что постоянный множитель можно выносить за знак предела.
7)Пусть на промежутке [a; b] между функциями  и
и 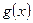 выполнено неравенство:
выполнено неравенство: 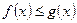 , тогда такое же неравенство будет выполнено между определенными интегралами этих функций по промежутку [a; b]
, тогда такое же неравенство будет выполнено между определенными интегралами этих функций по промежутку [a; b] 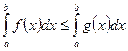 .
.
Доказательство: 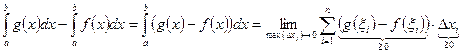 , тогда, по теореме о предельном переходе в неравенствах получаем, что предел больше или равен нуля.
, тогда, по теореме о предельном переходе в неравенствах получаем, что предел больше или равен нуля.
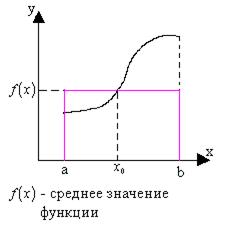
Теорема о среднем.
Пусть на промежутке [a; b] имеется функция  и, функция
и, функция 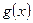 определена и сохраняет знак на промежутке [a; b], тогда внутри промежутка [a; b] найдется такая точка х0, что будет выполнено следующее неравенство:
определена и сохраняет знак на промежутке [a; b], тогда внутри промежутка [a; b] найдется такая точка х0, что будет выполнено следующее неравенство: 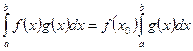 .
.
Доказательство:
1) 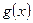 ≥ 0, тогда поскольку функция
≥ 0, тогда поскольку функция  непрерывна, то из теоремы Вейерштрасса вытекает, что она принимает на промежутке [a; b] свое наибольшее и наименьшее значения, т.е.
непрерывна, то из теоремы Вейерштрасса вытекает, что она принимает на промежутке [a; b] свое наибольшее и наименьшее значения, т.е. 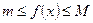 .
.
Тогда, домножая на неотрицательную функцию 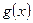 , получим:
, получим: 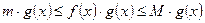
Используя свойство №7 получим: 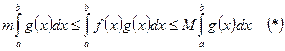
Дальше возможны два случая:
а) 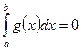 , тогда утверждение теоремы вытекает из неравенства (*).
, тогда утверждение теоремы вытекает из неравенства (*).
б) Пусть 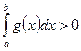 , тогда разделим на этот интеграл неравенство (*)
, тогда разделим на этот интеграл неравенство (*)
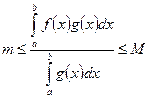 , но тогда, по второй теореме Коши о непрерывных функциях, в какой-то точке х0 значение функции в точности равно
, но тогда, по второй теореме Коши о непрерывных функциях, в какой-то точке х0 значение функции в точности равно  , т.е.
, т.е. 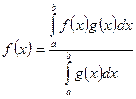
2) 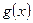 < 0
< 0
записывая теорему о среднем для функции - 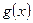 и затем убирая знак (-) получаем, что доказан и этот случай.
и затем убирая знак (-) получаем, что доказан и этот случай.
Следствие: пусть 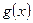 =1, тогда
=1, тогда 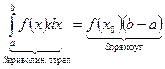
Дата добавления: 2016-06-24; просмотров: 797;
