Интегрирование по частям.
Справедлива следующая формула: 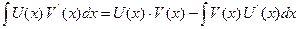
Замечание: для запоминания удобнее следующая символическая запись: 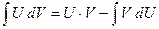
Доказательство:
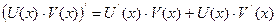 . Найдем неопределённый интеграл от правой и левой части равенства:
. Найдем неопределённый интеграл от правой и левой части равенства: 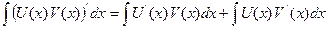 . По одному из свойств можно заменить левую часть на
. По одному из свойств можно заменить левую часть на 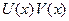 . Произвольную постоянную можно не писать в равенстве до тех пор, пока есть хотя бы один знак неопределённого интеграла. Неопределённый интеграл всегда содержит произвольную постоянную, а от сложения любого числа произвольных постоянных снова получится произвольная постоянная.
. Произвольную постоянную можно не писать в равенстве до тех пор, пока есть хотя бы один знак неопределённого интеграла. Неопределённый интеграл всегда содержит произвольную постоянную, а от сложения любого числа произвольных постоянных снова получится произвольная постоянная.
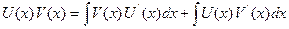 из этого равенства выразим:
из этого равенства выразим: 
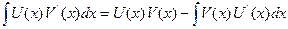
Замечание:
1) Формулу интегрирования по частям имен смысл применять в тех случаях, когда интеграл в правой части формулы проще исходного.
2) Подынтегральное выражение разбивается на произведение двух частей; одна из них ‘U’, как правило, упрощается после взятия производной. Оставшаяся часть ‘dV’, не усложняется после интегрирования.
Пример:
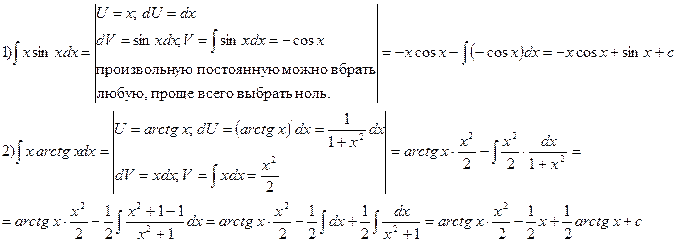 Замечание:
Замечание:
1) Часто формулу интегрирования по частям необходимо применять многократно.
2) Часто помогают следующие рекомендации:
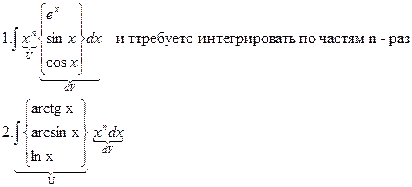
Дата добавления: 2016-06-24; просмотров: 878;
