Интегрирование рациональных дробей по методу Остроградского
Мы видели, что интегрирование некоторых рациональных дробей часто связано с утомительными выкладками.
Метод Остроградского значительно сокращает и упрощает интегрирование этих дробей, что делает этот метод ценным.
В основе указанного метода лежит следующая формула Остроградского:
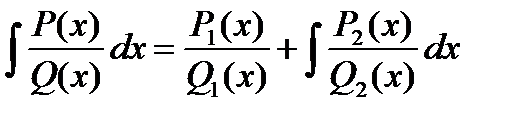 ,
,
Где 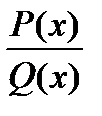 - правильная несократимая рациональная дробь;
- правильная несократимая рациональная дробь;
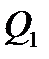 - общий наибольший делитель многочлена
- общий наибольший делитель многочлена 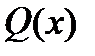 его производной
его производной 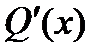 ;
;
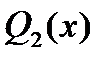 - частное от деления
- частное от деления 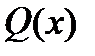 на
на 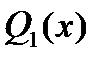 ;
;
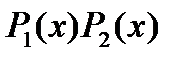 - неизвестные многочлены, степень каждого из которых по крайней мере на единицу ниже соответствующего знаменателя; при этом
- неизвестные многочлены, степень каждого из которых по крайней мере на единицу ниже соответствующего знаменателя; при этом 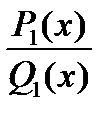 называется рациональной частью интеграла.
называется рациональной частью интеграла.
Как практически выполняется интегрирование правильных рациональных дробей с помощью метода Остроградского, покажем на примере:
Пример6.6.60. 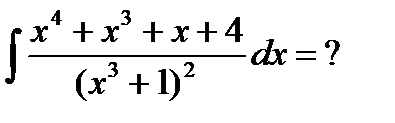 ;
;
Применяем метод Остроградского. Здесь 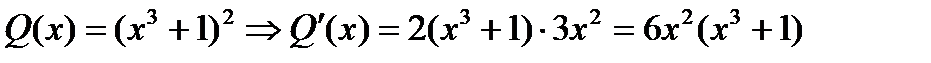 ;
;
Поэтому наибольший общий делитель: 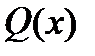 и
и 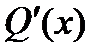 есть
есть 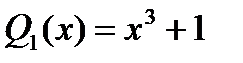 ;
;
Тогда 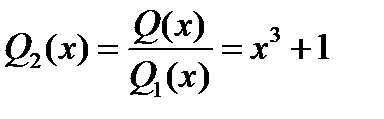 ;
;
Следовательно, согласно формуле Остроградского, мы будем иметь:
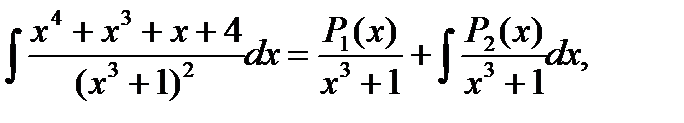 где
где 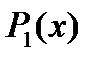 и
и 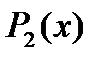 - многочлены степени не выше второй.
- многочлены степени не выше второй.
Напишем их с неопределенным коэффициентом
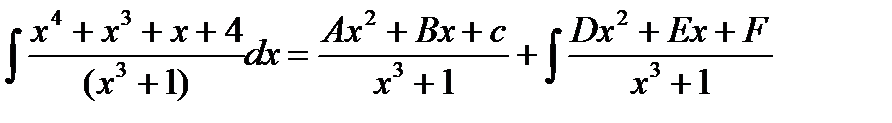
Дифференцируя обе части этого равенства найдем:
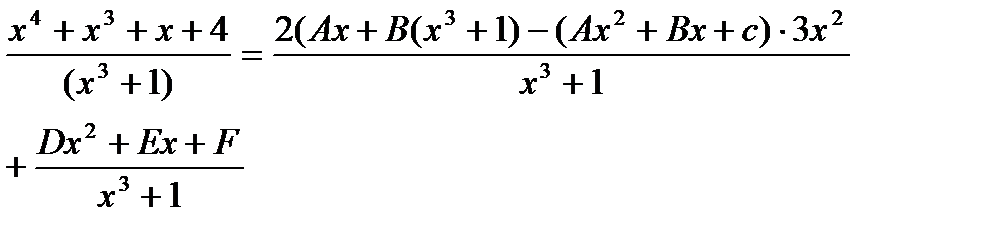 ;
;
Освобождаясь от знаменателя, получим тождество:
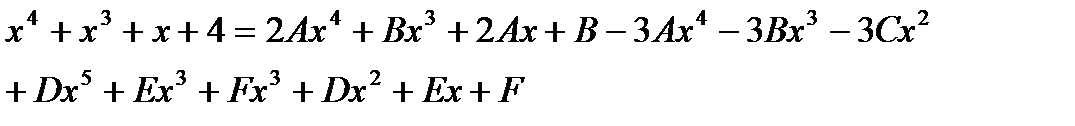 .
.
Приравнивая коэффициенты при одинаковых степенях х в правой и левых частях этого тождества, получим систему уравнений:
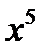
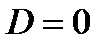 , Решая ее, найдем:
, Решая ее, найдем:
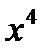
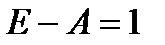 ,
, 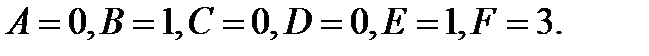
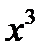
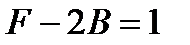 ,
,
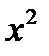
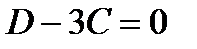 ,
,
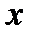
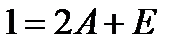 ,
,
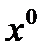
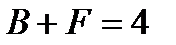 . Следовательно
. Следовательно
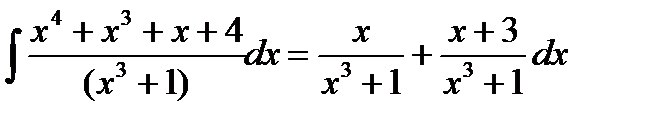 .
.
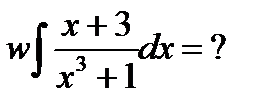 ;
; 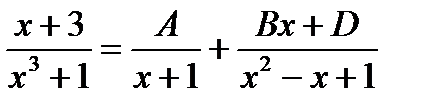 ;
; 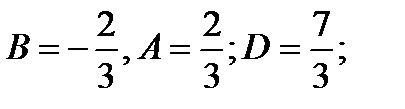
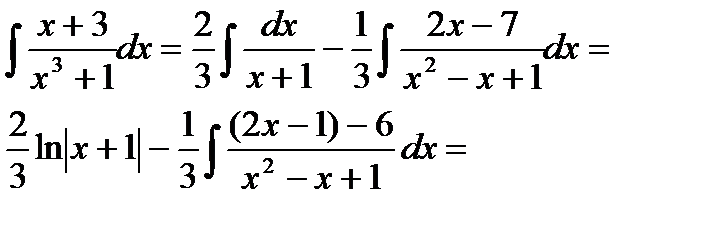 и т.д.
и т.д.
Подстановки Эйлера
Интегралы вида 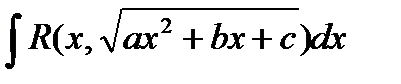
Где 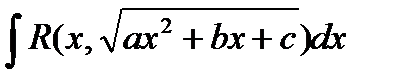 - рациональная относительно
- рациональная относительно 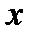 и
и 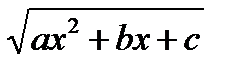 функция;
функция;
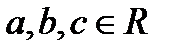 ; могут быть вычислены с помощью специальных рационализирующих подстановок, называемых подстановками Эйлера.
; могут быть вычислены с помощью специальных рационализирующих подстановок, называемых подстановками Эйлера.
Вообще, для вычисления интегралов этого вида существует много различных приемов, например, тригонометрические подстановки и другие, о которых шла речь выше.
Рассмотрим эти подстановки:
1-я подстановка Эйлера.
Так называется подстановка 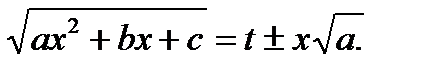
Она применяется, если 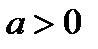
Обе указанные разновидности этой подстановки (со знаком «+» и со знаком «-») однотипны (вопрос о том, какая из них удобнее, решается в каждом отдельном случае по-своему).
Рассмотрим одну из них: 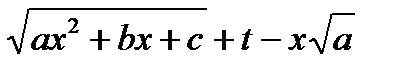 ; возводя обе части в получим:
; возводя обе части в получим:
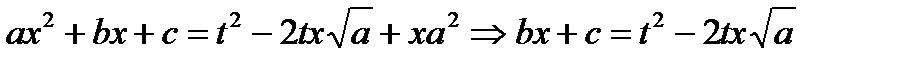
видим, что член  уничтожается – в этом “соль” данной подстановки
уничтожается – в этом “соль” данной подстановки
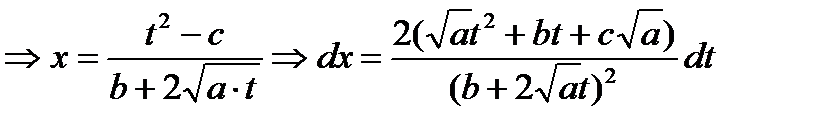 .
.
Тогда 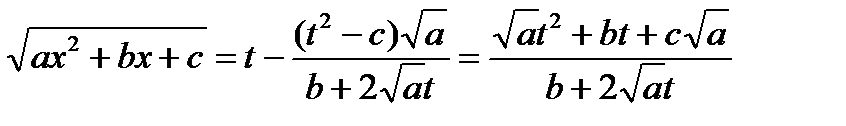 ;
;
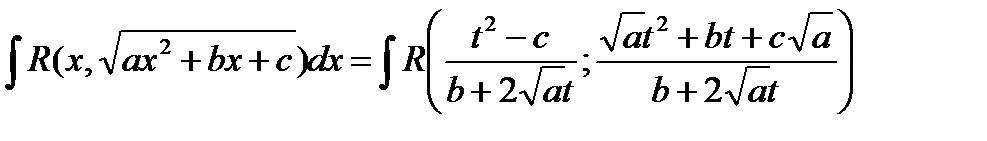 .
.
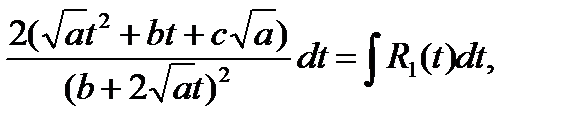 т.е. вопрос свелся к интегрированию рациональной функции
т.е. вопрос свелся к интегрированию рациональной функции
Пример6.6.61. 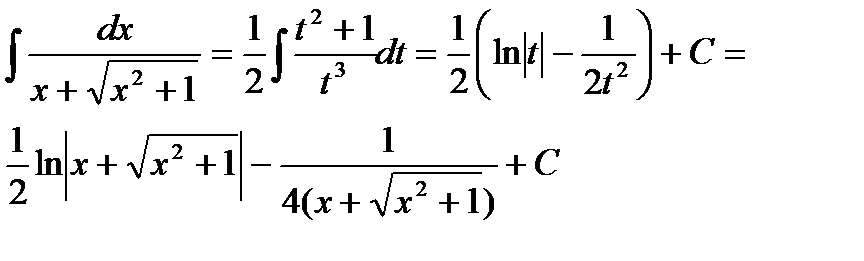 .
.
Где, 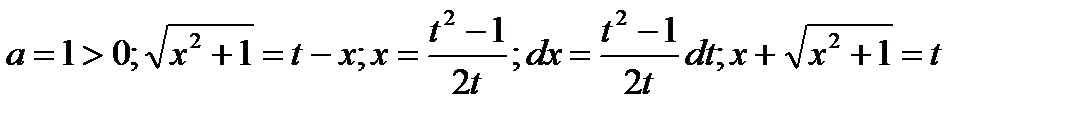 .
.
2-я подстановка Эйлера:
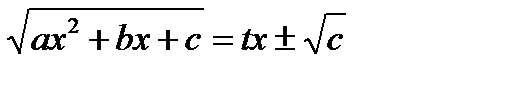 ;
;
Она применяется, когда 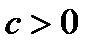
Пусть 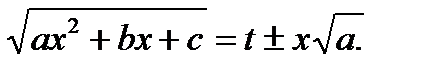
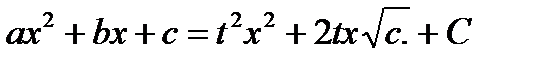
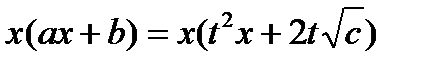 ,
, 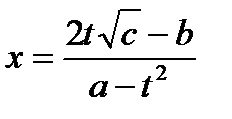
Откуда видно, что 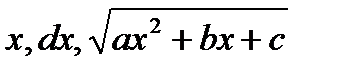 рационально выражаются через t и dt.
рационально выражаются через t и dt.
Пример6.6.62. 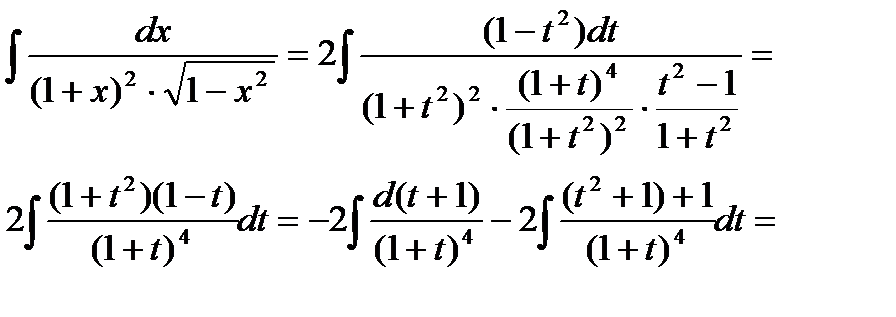
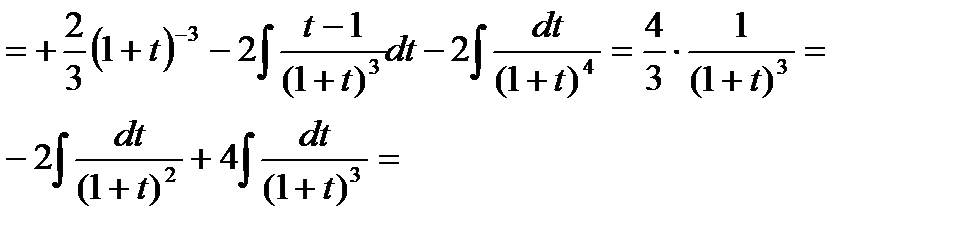
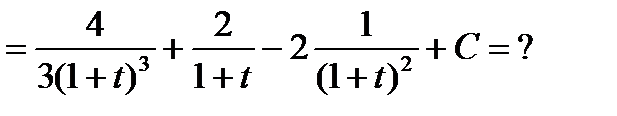 где
где 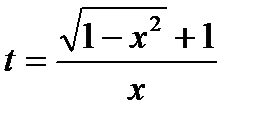
3 -я подстановка Эйлера:
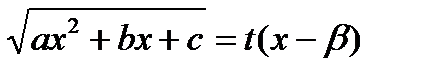
Пусть 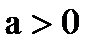 , но корни трехчлена
, но корни трехчлена 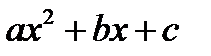 действительны (если корни мнимые, то трехчлен при любом значении
действительны (если корни мнимые, то трехчлен при любом значении 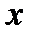 – при
– при 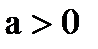 - отрицателен).
- отрицателен).
Пусть 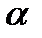 и
и 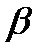 - корни трехчлена, кроме того, пусть
- корни трехчлена, кроме того, пусть 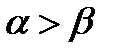 .
.
Пример6.6.63. 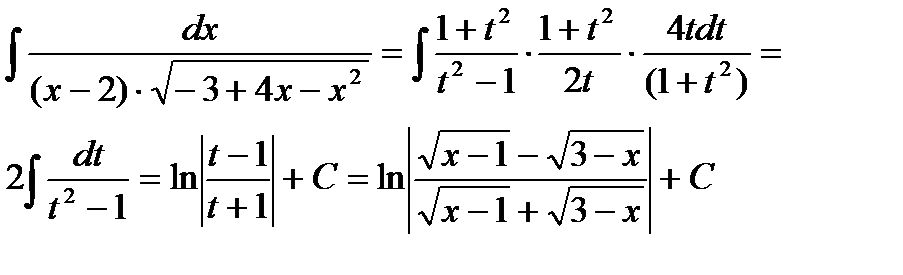
Где, 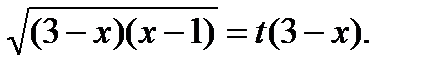
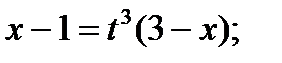
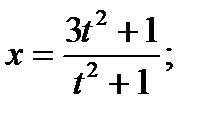
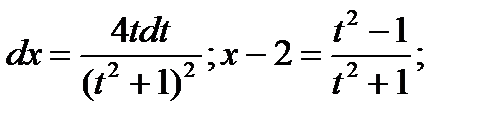
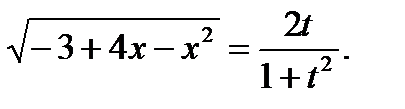

Дата добавления: 2016-10-17; просмотров: 1158;
