Понятие определенного интнграла

Пусть на [a;b] задана непрерывная функция у =f(x).

Разобьем отрезок [a; b] на n частичных отрезков с помощью произвольно выбранных на нем точек .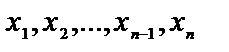

На каждом из отрезков (частичных) возьмем произвольные точки ξ_i (i=1,2,3…n). Во взятых точках вычислим значения функции f(x): f(ξ₁), f(ξ₂), f(ξ₃)…, f(ξ_n).

Составим произведения длин ∆x₁ , ∆x₂, …,∆x_n частичных отрезков на значения функции f(ξ_i).

Все эти произведения сложим и выразим сумму их через

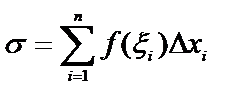(6.7.1)

где σ=f(ξ₁)∆х₁+f(ξ₂) ∆х₂+f(ξ₃)∆х₃+…+ f(ξ_n)∆х_n; или

Сумму такого вида называют интегральной суммой, составленной для функции f(x)на отрезке [a;b].

Будем неограниченно увеличивать число делений отрезка [a;b]однако так, чтобы длина ∆x_iкаждого отрезка [x_i-1;x] стремилась к нулю; и рассмотрим получающееся при этом множество интегральных сумм σ.

Еслипри этом разбиении интегральные суммы будут стремиться к одному и тому же пределу, то этот предел называют определенным интегралом от функции f(x)на отрезке[a;b].

Определение.

Если существует пределсуммы (1) при ∆х_i→0, то говорят, что функция f(x) интегрируема на [a;b], число I называют определенным интегралом от функции f(x) на [a;b]. ,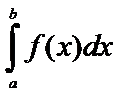

где числа «а» и «b» называются пределами интегрирования (или интеграла), соответственно нижним, верхним; отрезок [a;b] – промежутком интегрирования.