Замена переменной в определенном интеграле
Пусть требуется вычислить 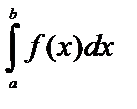 , где f(x)- непрерывная на [a;b] функция. Часто здесь бывает удобно применить, как и в случае вычисления неопределенного интеграла, замену переменной путем введения вместо старой переменной новой переменной t, связанной со старой соотношением
, где f(x)- непрерывная на [a;b] функция. Часто здесь бывает удобно применить, как и в случае вычисления неопределенного интеграла, замену переменной путем введения вместо старой переменной новой переменной t, связанной со старой соотношением 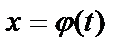 .
.
Итак, введем новую переменную t, положив 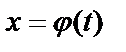 .
.
Пусть выполняются следующие условия:
а) функция 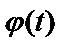 определена и непрерывна на отрезке
определена и непрерывна на отрезке 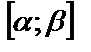 ;
;
б) при изменении tна 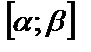 значения функции
значения функции 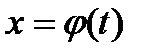 не выходят за пределы отрезка
не выходят за пределы отрезка 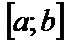 . При этом
. При этом 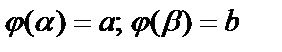 ;
;
в) Функция 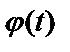 на отрезке
на отрезке 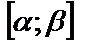 имеет непрерывную производную
имеет непрерывную производную 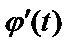 .
.
Тогда имеет место равенство
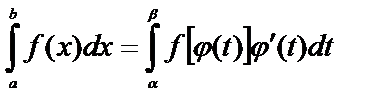 (6.7.4)
(6.7.4)
При пользовании формулой (6.7.4) следует функцию 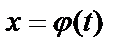 стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
Пример 6.7.3.Вычислить: 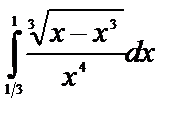
Решение: применим подстановку: 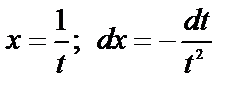 . Найдем пределы интегралов для новой переменной при
. Найдем пределы интегралов для новой переменной при 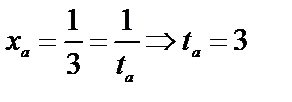 , при
, при 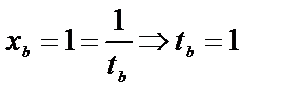 .
.
Следовательно, при применении x от1/3 до 1 новая переменная t изменяется от 3 до 1.
Функция 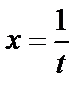 - убывает и непрерывна вместе со своей производной
- убывает и непрерывна вместе со своей производной
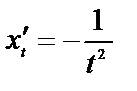 на отрезке
на отрезке 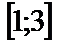
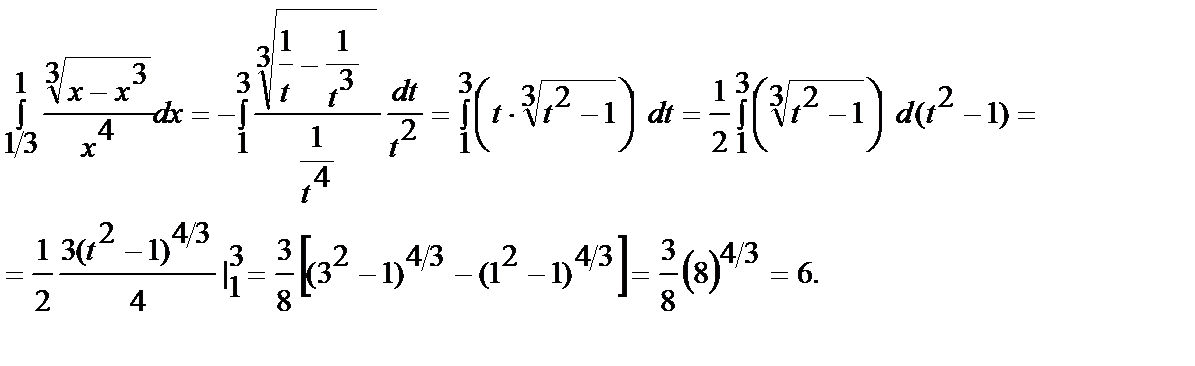
Пример 6.7.4. Вычислить: 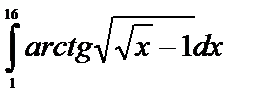 .
.
Решение.
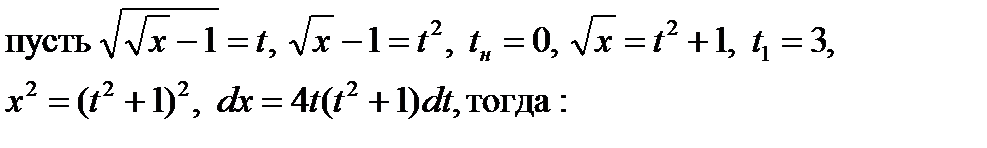
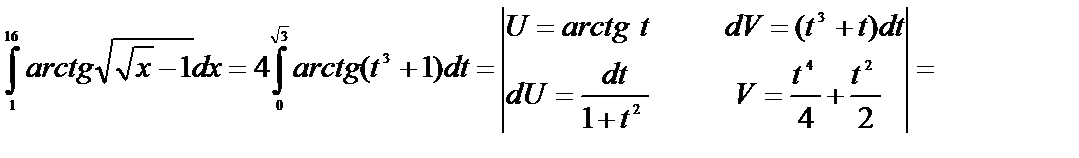
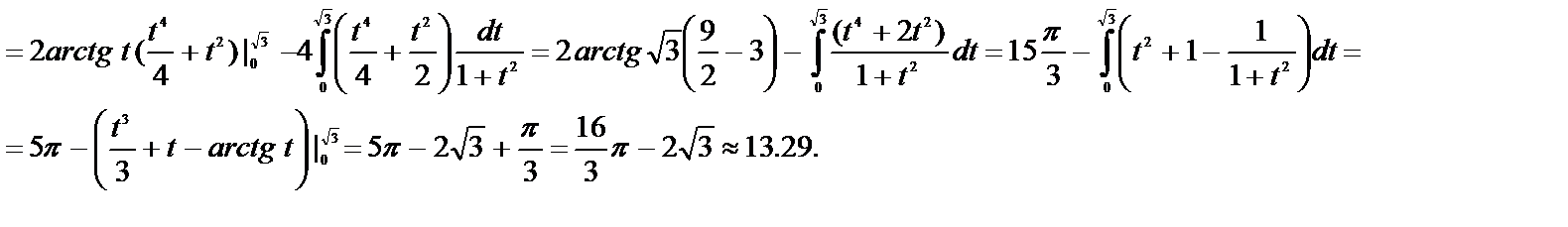
Дата добавления: 2016-10-17; просмотров: 665;
