Дифференциальное исчисление функции одной переменной
1. Введение
Математический анализ – ветвь математики, оформившаяся в ХVIII столетии и включающая в себя две основные части: дифференциальное и интегральное исчисления. Производная функции – одно из основных математических понятий дифференциального исчисления. Анализ возник благодаря усилиям многих математиков (в первую очередь И. Ньютона и Г. Лейбница) и сыграл громадную роль в развитии естествознания – появился мощный, достаточно универсальный метод исследования функций, возникающих при решении разнообразных прикладных задач.
2. Числовая функция. Схема исследования функции.
(Смотри конспекты по теме «Степенная функция»)
1) Область определения функции.
2) Множество значений функции.
3) Четность, нечетность функции.
4) Монотонность функции.
5) Обратимость функции.
6) Нули функции.
7) Промежутки знакопостоянства функции.
8) Ограниченность функции.
Упражнения:
- Найти область определения функции:
а) 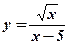 ; б)
; б) 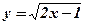 ; в)
; в) 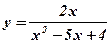 .
.
- Найти область определения функции: а)
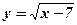 ; б)
; б) 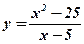 .
. - Выяснить, является ли функция четной или нечетной:
а) 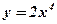 ; б)
; б) 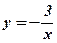 ; г)
; г) 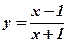 .
.
3. Понятие предела функции в точке.
Рассмотрим графики некоторых функций. Изучим поведение функций вблизи точки х0 , то есть в некоторой окрестности точки х0.
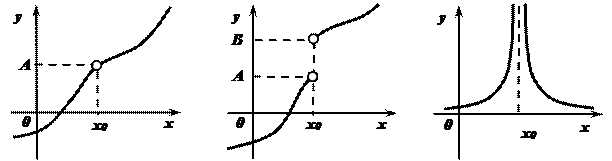 |
Рис. 1. 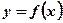 Рис. 2.
Рис. 2. 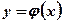 Рис. 3.
Рис. 3. 
Функция 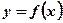 обладает свойством, отличающим ее от двух других функций.
обладает свойством, отличающим ее от двух других функций.
1. При приближении аргумента х к х0 слева и справа соответствующие значения функции 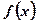 сколь угодно близки к одному и тому же числу А.
сколь угодно близки к одному и тому же числу А.
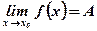
Этим свойством не обладают две другие функции.
2. При приближении аргумента х к х0 слева соответствующие значения функции 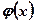 сколь угодно близки к числу А, а при приближении аргумента х к х0 справа соответствующие значения функции
сколь угодно близки к числу А, а при приближении аргумента х к х0 справа соответствующие значения функции 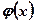 сколь угодно близки к числу В.
сколь угодно близки к числу В.
3. Функция 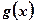 при приближении аргумента х к х0 слева и справа принимает различные значения.
при приближении аргумента х к х0 слева и справа принимает различные значения.
Вывод:Еслипри приближении аргумента х к х0 слева и справа точки с координатами 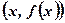 сколь угодно близки к точке с координатами
сколь угодно близки к точке с координатами 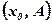 , то
, то 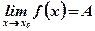 .
.
Пример: Имеет ли функция 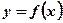 предел в точках х1, х2, х3, х4, х5?
предел в точках х1, х2, х3, х4, х5?
 |
Ответ: Функция 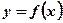 имеет предел в точках х1, х3 ;
имеет предел в точках х1, х3 ;
функция 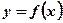 не имеет предела в точках х2, х4, х5.
не имеет предела в точках х2, х4, х5.
Замечание: 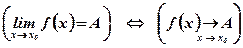
4. Определение функции непрерывной в точке и на промежутке
Понятие непрерывности функции удобно связать с представлением о графике этой функции как о «неразрывной» (сплошной) линии. Сплошной линией будем считать линию, начерченную без отрыва карандаша от бумаги.
Вопрос: Какие из данных функций являются непрерывными?

 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.
Рис. 4. Рис. 5.
Ответ: Из данных функций непрерывной является функция, изображенная на рис. №3, так как ее график - «неразрывная» (сплошная) линия.
Вопрос: Какими свойствами обладает функция, изображенная на рис. №3, и не обладают другие функции?
Ответ:
1. Функция определена в точке х0. Это свойство не выполняется для функции, изображенной на рис. №1.
2. Существует конечный предел функции в точке х0. Это свойство не выполняется для функций, изображенных на рис. №2, 5.
3. Предел функции в точке х0 равен значению функции в этой точке, то есть 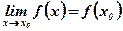 . Это свойство не выполняется для функции, изображенной на рис. №4.
. Это свойство не выполняется для функции, изображенной на рис. №4.
Свойства, которые выполняются для функции, изображенной на рис. №3, и дают возможность дать определение функции непрерывной в точке х0.
Определение: Функция 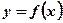 называется непрерывной в точке х0, если
называется непрерывной в точке х0, если 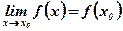 .
.
Замечание: Если функция является непрерывной в точкех0,то точка х0 называется точкой непрерывности функции, если функция не является непрерывной в точкех0,то точка х0 называется точкой разрыва функции.
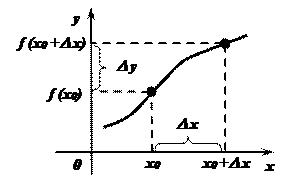 Определение: Функция
Определение: Функция 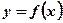 называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
5. Приращение аргумента, приращение функции
Пусть задана функция 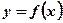 ,
, 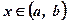 .
.
х0 – начальное значение аргумента, 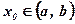 ;
;
х– конечное значение аргумента, 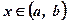 ;
;
f (х0) – начальное значение функции;
f(х0 +D х) – конечное значение функции.
Определение: Разность конечного и начального значений аргумента называется приращением аргумента. D х = х – х0
Определение: Разность конечного и начального значений функции называется приращением функции. D у = f(х0 +D х) – f (х0)
Замечание:
- Геометрически приращение аргумента D х– есть разность абсцисс точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Геометрически приращение функции D у– есть разность ординат точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Приращение аргумента и приращение функции могут быть как положительными, так и отрицательными.
6. Понятие производной функции. Физический смысл производной функции
Рассмотрим задачу о скорости изменения функции 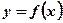 , где х и у могут быть любыми физическими величинами.
, где х и у могут быть любыми физическими величинами.
х0 – начальное значение аргумента; f (х0) – начальное значение функции;
х0 +D х – конечное значение аргумента; f(х0 +D х) – конечное значение функции;
D у = f(х0 +D х) – f (х0) – приращение функции;
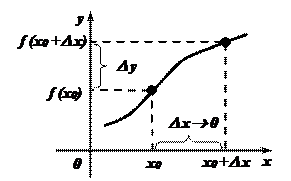
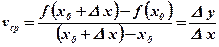
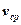 – средняя скорость изменения функции на интервале D х.
– средняя скорость изменения функции на интервале D х.
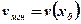 – мгновенная скорость изменения функции, скорость изменения функции в точке х0.
– мгновенная скорость изменения функции, скорость изменения функции в точке х0.
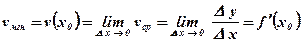
Определение: Производной функции 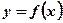 в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
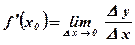
Вывод: Производная функции 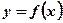 в точке х0 есть скорость изменения функции в точке х0.
в точке х0 есть скорость изменения функции в точке х0.
Теорема: Производная постоянной функции у = с в любой точке 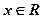 равна нулю.
равна нулю.
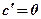
Теорема: Производная функции у = х в любой точке 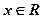 равна единице.
равна единице.
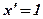 .
.
Замечание: Нахождение производной от данной функции называется дифференцированием.
7. Правила дифференцирования суммы, произведения, частного функций
Рассмотрим функцию 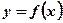 ,состоящую из двух других функций
,состоящую из двух других функций 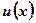 и
и 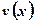 , имеющих производные на отрезке
, имеющих производные на отрезке 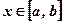 :
:
1) 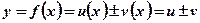 ;
;
2) 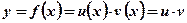 ;
;
3) 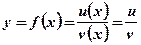 .
.
Теорема №1: Производная суммы (разности) двух функций равна сумме (разности) производных этих функций. 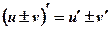
Пример: Вычислить производную функции 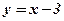
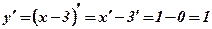 ;
; 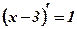 .
.
Теорема №2: Производная произведения двух функций определяется по формуле: 
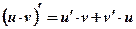
Следствие: Постоянный множитель можно вынести за знак производной: 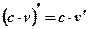 .
.
Доказательство: 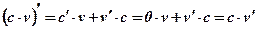 .
.
Пример: Вычислить производные функций:
-
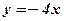 .
. 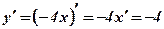 .
. -
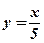 .
. 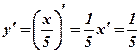 .
. -
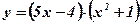 .
.
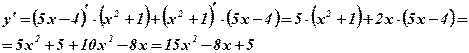
-
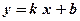 .
. 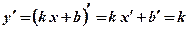 ;
; 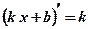 .
.
Упражнения:
1) 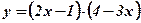 ;
;
2) 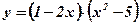 ;
;
3) 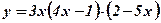 .
.
Производная степенной функции 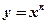 при
при 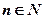 вычисляется по формуле:
вычисляется по формуле:
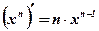
Замечание: Формула 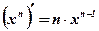 справедлива для степенной функции с любым показателем степени
справедлива для степенной функции с любым показателем степени 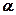 .
. 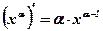 ,
, 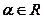
Пример: Вычислить производные функций:
-
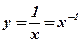 . Решение:
. Решение: 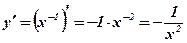 .
. -
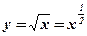 . Решение:
. Решение: 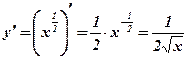 .
. -
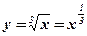 . Решение:
. Решение: 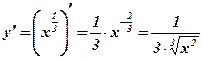 .
. -
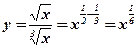 . Решение:
. Решение: 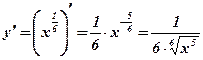 .
.
Вывод: 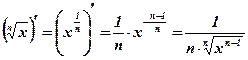 .
.
Упражнения: Вычислить производные функций:
1) 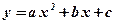 ;
2) ;
2) 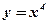 ;
3) ;
3) 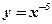 ; ;
| 4) 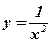 ;
5) ;
5) 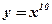 ; ;
| 6) 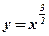 ;
7) ;
7) 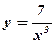 . .
|
Теорема №3: Производная частного двух функций определяется по формуле: 
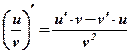
Следствия: 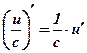 ;
; 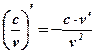
Пример: Вычислить производные функций:
1) 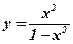 .
.
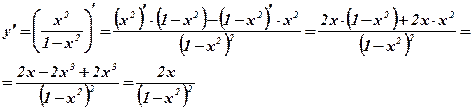
2) 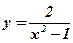 .
. 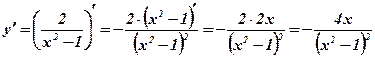 .
.
3) 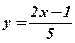 .
. 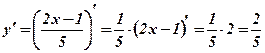 .
.
Упражнения: Вычислить производные функций:
1. 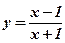 ;
2. ;
2. 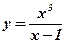 ;
3. ;
3. 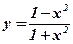 ; ;
| 4. 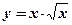 ;
5. ;
5. 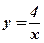 ;
6. ;
6. 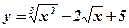 ; ;
| 7. 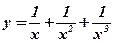 ;
8. ;
8. 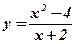 ;
9. ;
9. 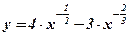 . .
|
8. Понятие сложной функции
Правило дифференцирования сложной функции
Пусть функция 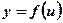 определена на множестве
определена на множестве 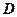 , а функция
, а функция 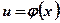 на множестве
на множестве 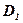 , причем для
, причем для 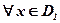 , соответствующее значение
, соответствующее значение 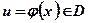 . Тогда на множестве
. Тогда на множестве 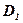 определена функция
определена функция 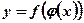 , которая называется сложной функцией от х(функцией от функции).
, которая называется сложной функцией от х(функцией от функции).
Переменную 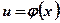 называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Пример:
-
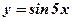 - тригонометрическая, линейная функция;
- тригонометрическая, линейная функция; 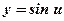 ,
, 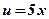 ;
; -
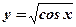 - степенная, тригонометрическая функция;
- степенная, тригонометрическая функция; 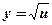 ,
, 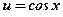 ;
; 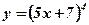 - степенная, линейная функция;
- степенная, линейная функция; 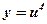 ,
, 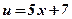 ;
;-
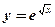 - показательная, степенная функция;
- показательная, степенная функция; 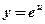 ,
, 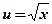 ;
;
Упражнения:
- Из каких элементарных функций состоят данные сложные функции:
1) 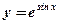 ;
2) ;
2) 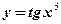 ; ;
| 3) 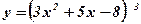 ;
4) ;
4) 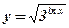 . .
|
- Из данных элементарных функций составить сложные функции:
1) 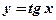 , , 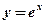 ;
2) ;
2) 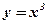 , , 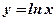 ; ;
| 3) 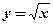 , , 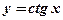 .
4) .
4) 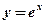 , , 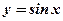 , , 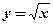 . .
|
Вывод: Производная сложной функции равна произведению производных элементарных функций, ее составляющих.
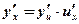
Пример: Вычислить производные функций:
1. 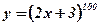 .
.
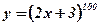 - степенная, линейная;
- степенная, линейная; 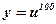 ,
, 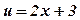 .
.
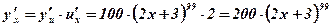 .
.
2. 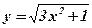 .
.
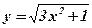 - степенная, квадратичная;
- степенная, квадратичная; 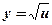 ,
, 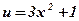 .
.
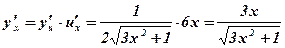 .
.
Упражнения: Вычислить производные функций:
1. 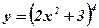 ;
2. ;
2. 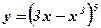 ; ;
| 3. 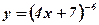 ;
4. ;
4. 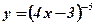 ; ;
| 5. 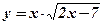 ;
6. ;
6. 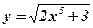 . .
|
9. Производная показательной, логарифмической функций
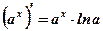
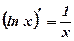
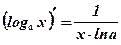
Пример: Вычислить производные функций:
1. 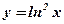 .
. 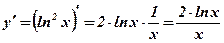 .
.
2. 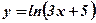 .
. 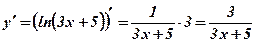 .
.
3. 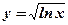 .
. 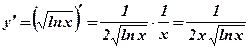 .
.
Пример: Вычислить производные функций:
1. 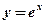 .
. 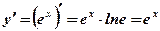 .
.
2. 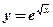 .
. 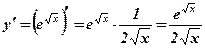 .
.
Упражнения: Вычислить производную функции:
1. 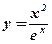 ;
2. ;
2. 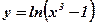 ;
3. ;
3. 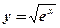 ; ;
| 4. 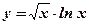 ;
5. ;
5. 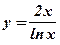 ;
6. ;
6. 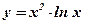 ; ;
| 7. 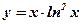 ;
8. ;
8. 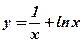 . .
|
10. Производные тригонометрических функций
Производные обратных тригонометрических функций
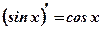 .
.
Пример: Вычислить производные функций:
1. 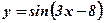 .
. 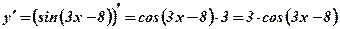 .
.
2. 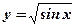 .
. 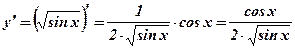 .
.
Задача: Вычислить производную функции 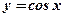 .
.
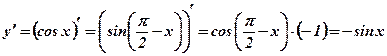 .
. 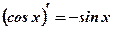 .
.
Задача: Вычислить производную функции 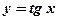 .
.
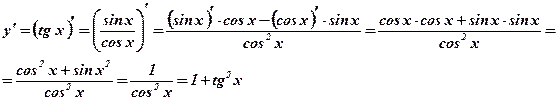
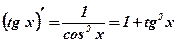 .
.
Упражнение: Вычислить производную функции 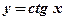 .
.
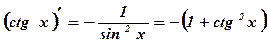 .
.
Дата добавления: 2016-05-25; просмотров: 936;
