Вычисление интегралов вида
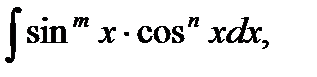
где 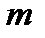 и
и 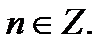
Здесь остановимся на следующих 3-х случаях:
1) 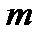 и
и 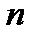 - четные неотрицательные числа.
- четные неотрицательные числа.
В этом случаи неопределенные интегралы находятся с помощью тригонометрических формул:
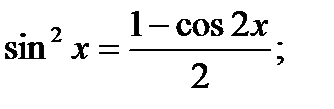
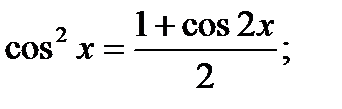
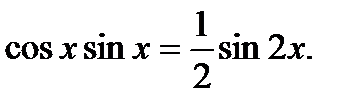
Пример 6.6.41. 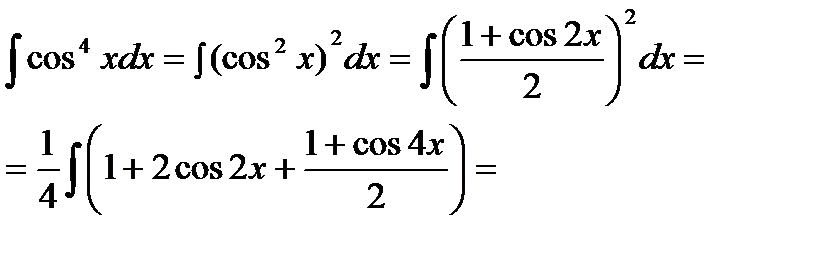
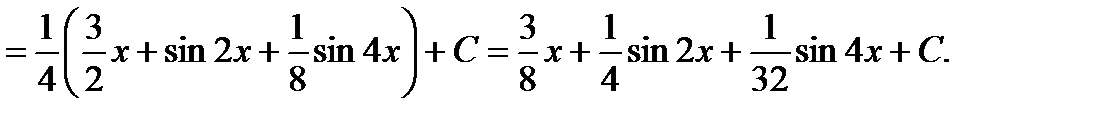
2)  или
или  - нечетное положительное число.
- нечетное положительное число.
Если хотя бы одно из чисел 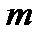 и
и 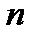 - нечетное, то от нечетной степени отделяется множитель и вводится новая переменная.
- нечетное, то от нечетной степени отделяется множитель и вводится новая переменная.
В частности, если 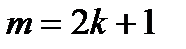 , то
, то 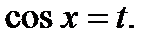
Другими словами, если показатель степени одной из тригонометрических функций – нечетное положительное число, то другую функцию принимают за t.
Пример6.6.42. 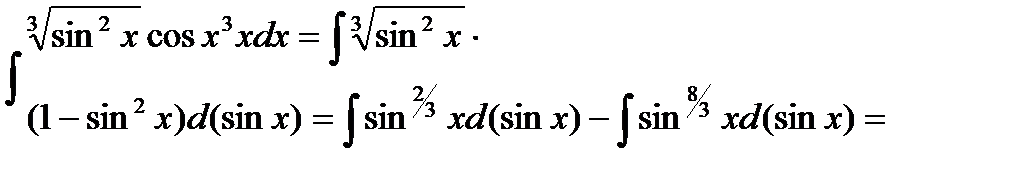
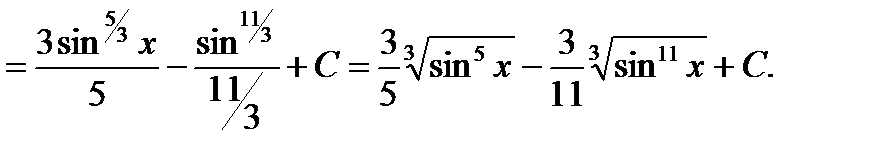
3) ) 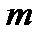 +
+ 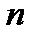 - четное отрицательное число.
- четное отрицательное число.
Если сумма показателей синуса и косинуса есть четное отрицательное число, подстановка 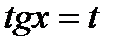 сводит интеграл к табличным (либо подстановка
сводит интеграл к табличным (либо подстановка 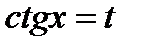 ).
).
Пример6.6.43.
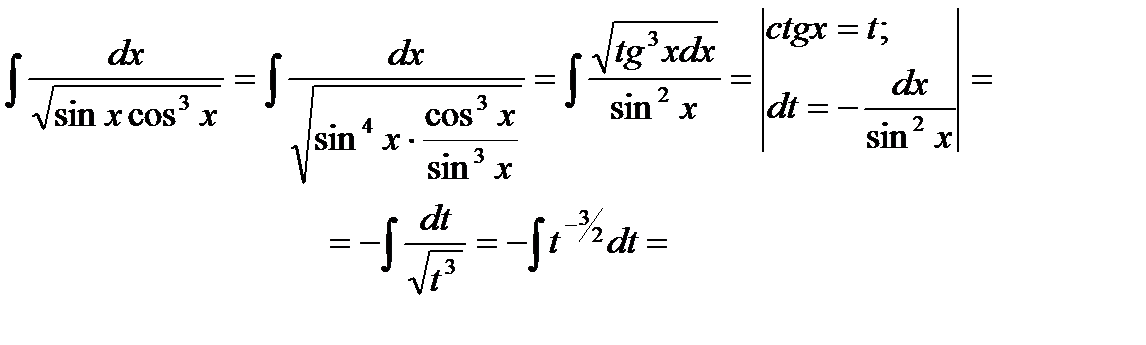
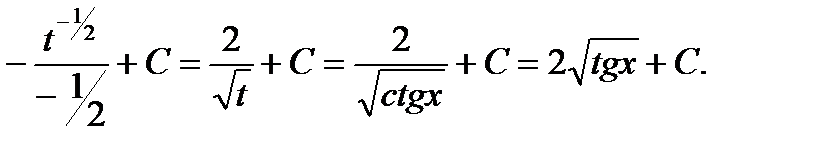
Пример 6.6.44. 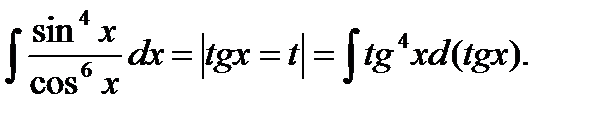
Остановимся на некоторых из них:
Пример6.6.45. 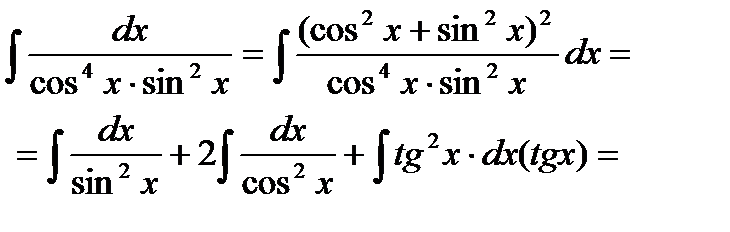
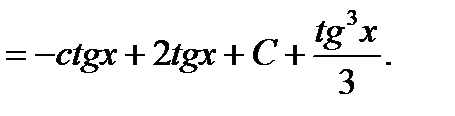 Однако целесообразнее ввести в числителе тригонометрическую единицу во второй степени.
Однако целесообразнее ввести в числителе тригонометрическую единицу во второй степени.
Пример 6.6.46. 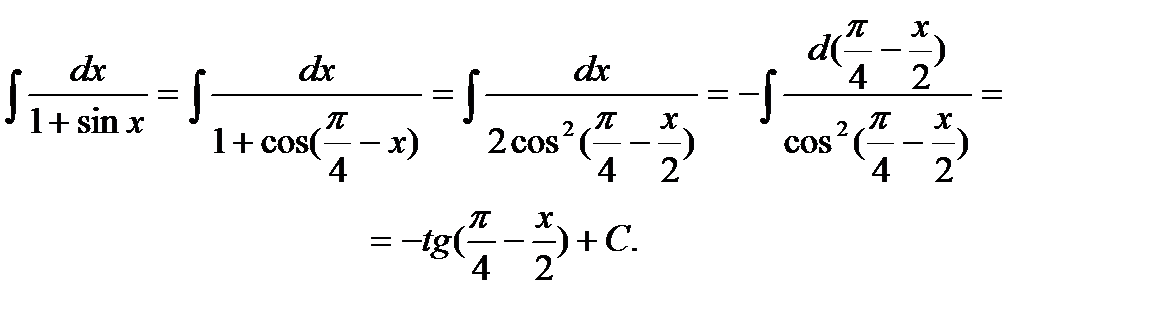
Пример 6.6.47. 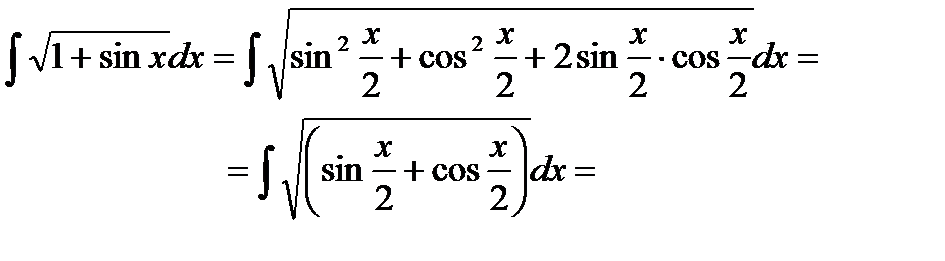
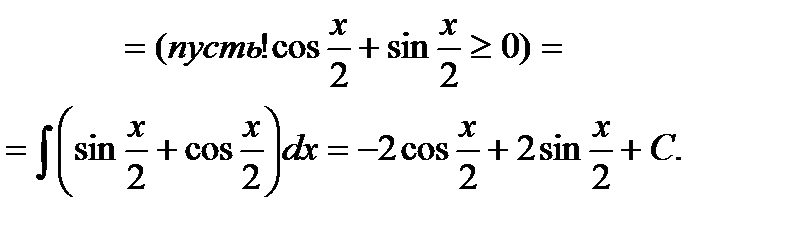
Пример 6.6.48.Вычисления с помощью универсальной подстановки 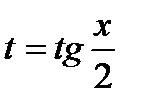 ; но она приводит к большим выкладкам.
; но она приводит к большим выкладкам.
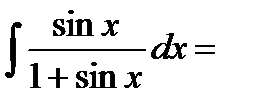
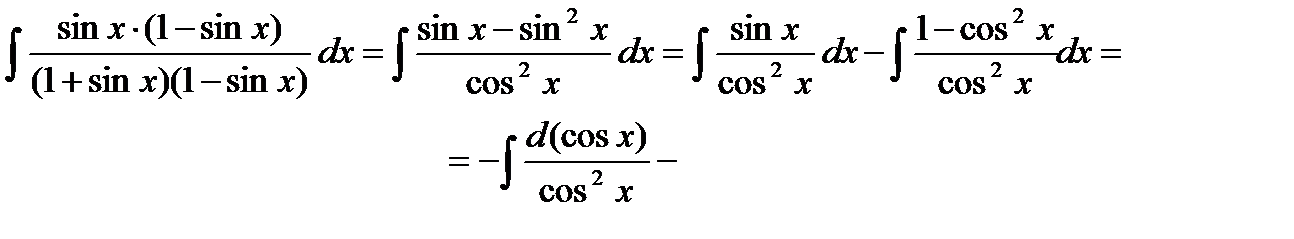
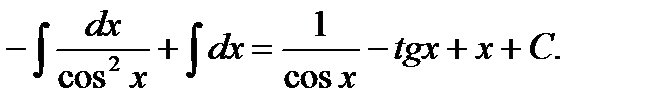
Примечание. Формулы понижения степени:
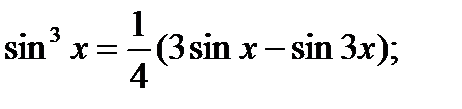
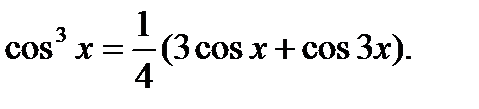
Тригонометрические подстановки
1) При вычислении интегралов вида 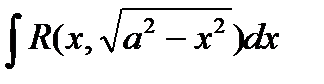
Где 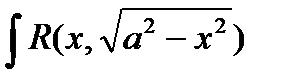 - рациональная функция относительно “х” и “
- рациональная функция относительно “х” и “ 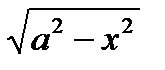 ” (то есть, когда подынтегральная функция содержит только радикалы вида
” (то есть, когда подынтегральная функция содержит только радикалы вида 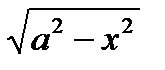 ) часто бывает полезна подстановка
) часто бывает полезна подстановка 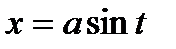 (или x = acost)
(или x = acost)
Любая из них приводит подынтегральную функцию к рациональному виду относительно sint и cost.
Пример6.6.49. 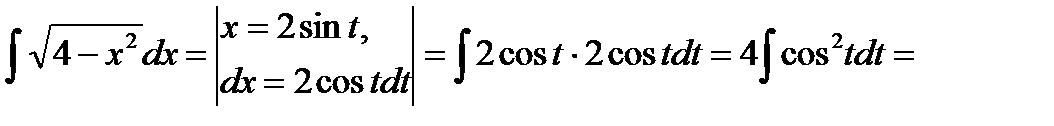 и т.д.
и т.д.
Пример6.6.50. 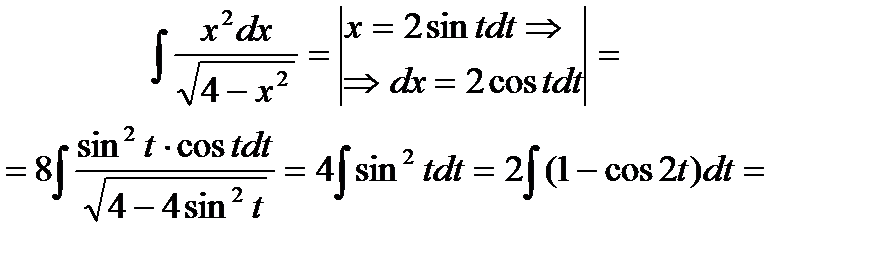
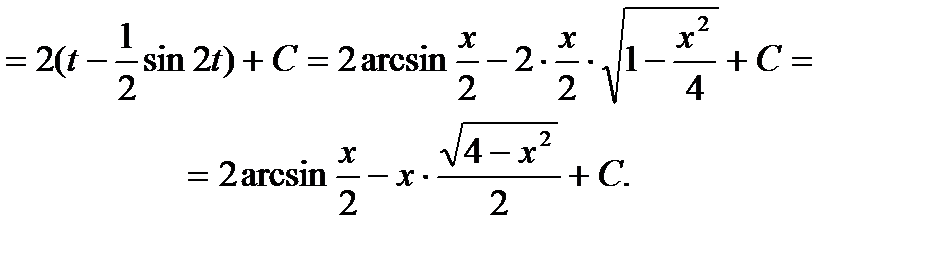
2) Интегралы вида рационализируется подстановкой.
Пример.
2) Интеграл вида 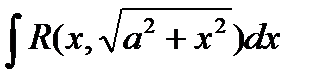 рационализируются подстановкой
рационализируются подстановкой 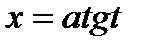
Пример 6.6.51. 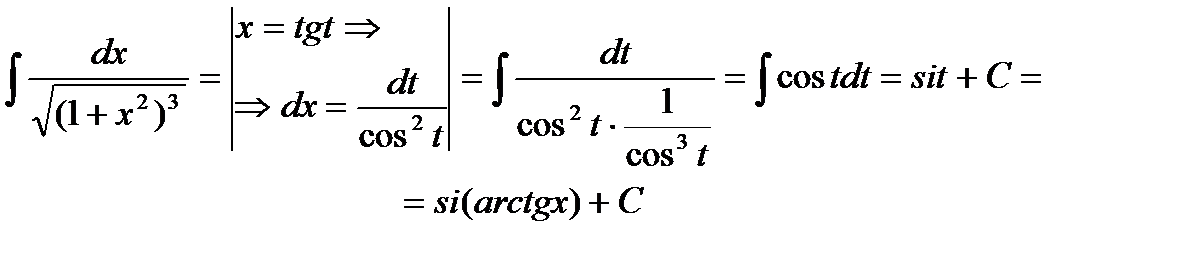
3) Интеграл вида 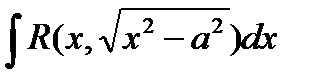
4) Применяется подстановка 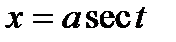
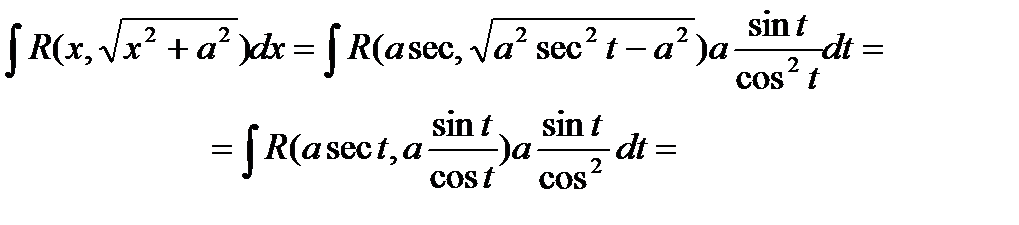

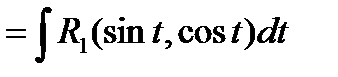
Пусть требуется вычислить 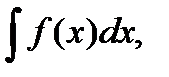 где
где 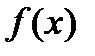 - некоторая алгебраическая явная иррациональная функция.
- некоторая алгебраическая явная иррациональная функция.
Здесь стараются подобрать такую подстановку (ее обычно называют рационализирующей) 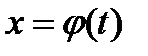 , чтобы функция
, чтобы функция 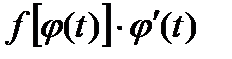 оказывалась рациональной.
оказывалась рациональной.
- Интегралы вида
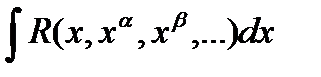 , где
, где 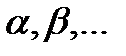 -рациональные числа
-рациональные числа 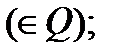
- R - рациональная функция от аргументов
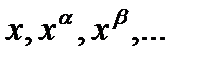
Для рационализации подынтегральной функции применяется подстановка 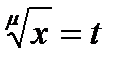 или
или 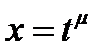 , где
, где 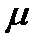 - общий знаменатель дробей
- общий знаменатель дробей 
( 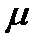 - общее наименьшее кратное показателей всех радикалов, под которыми х входят в подынтегральную функцию).
- общее наименьшее кратное показателей всех радикалов, под которыми х входят в подынтегральную функцию).
Подстановка 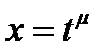 рационализирует рассматриваемый интеграл, то есть сводит его к интегралу рациональной дроби:
рационализирует рассматриваемый интеграл, то есть сводит его к интегралу рациональной дроби: 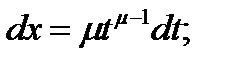
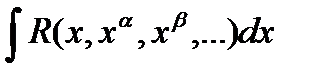 = после введения ‘t’, каждая дробная степень х выразиться через целую степень ‘t’, и, следующая подынтегральная функция будет рациональной относительно переменной ‘t’
= после введения ‘t’, каждая дробная степень х выразиться через целую степень ‘t’, и, следующая подынтегральная функция будет рациональной относительно переменной ‘t’ 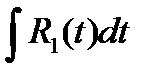
Пример6.6.52. 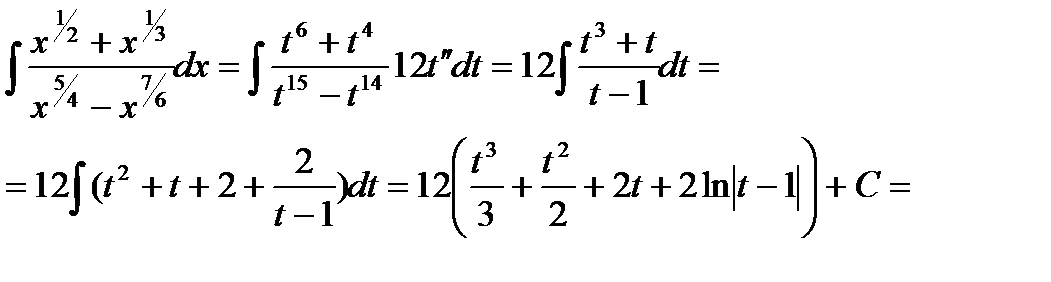
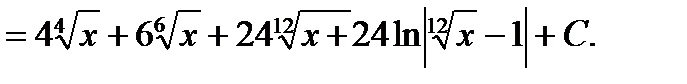 Где
Где 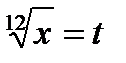
2. 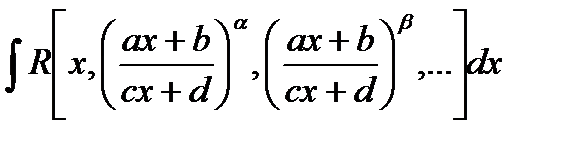 где
где 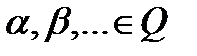 (т.е. рациональные числа);
(т.е. рациональные числа);
 .
.
Интегралы этого вида рационализируются подстановкой 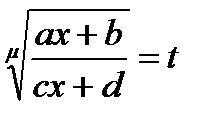 , или
, или 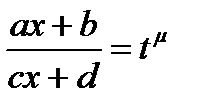 ,
,
Где 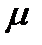 - общий знаменатель дробей
- общий знаменатель дробей 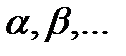
Вопрос сводится к интегрированной рациональной функции  .
.
Пример 6.6.53.
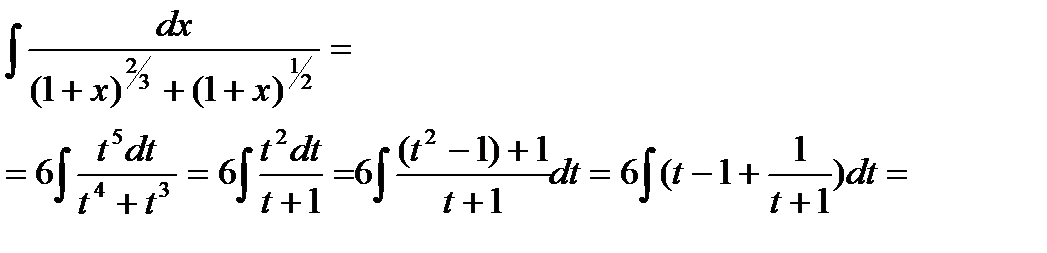
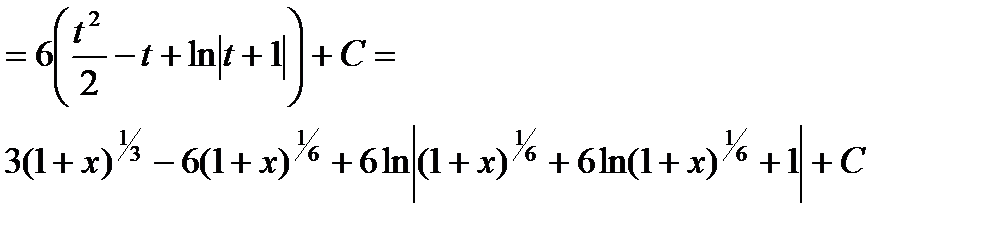 .
.
Пример 6.6.54. 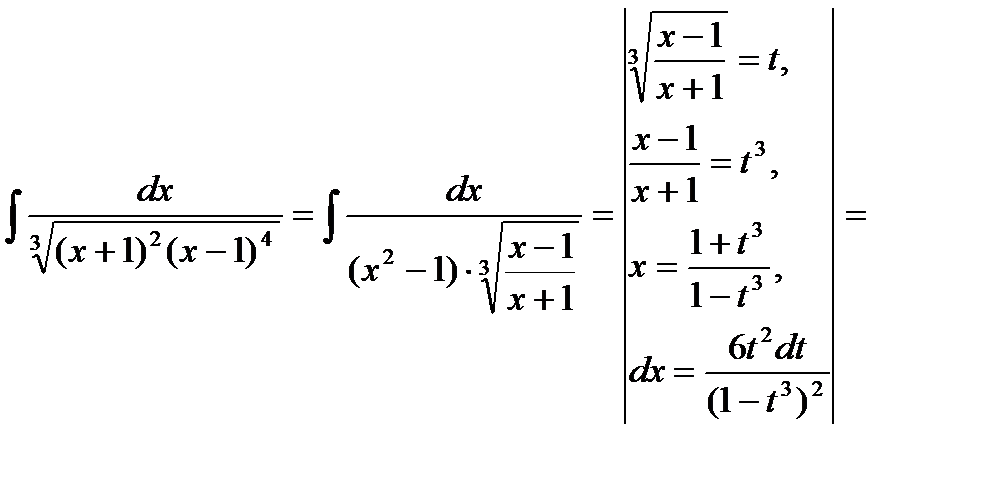
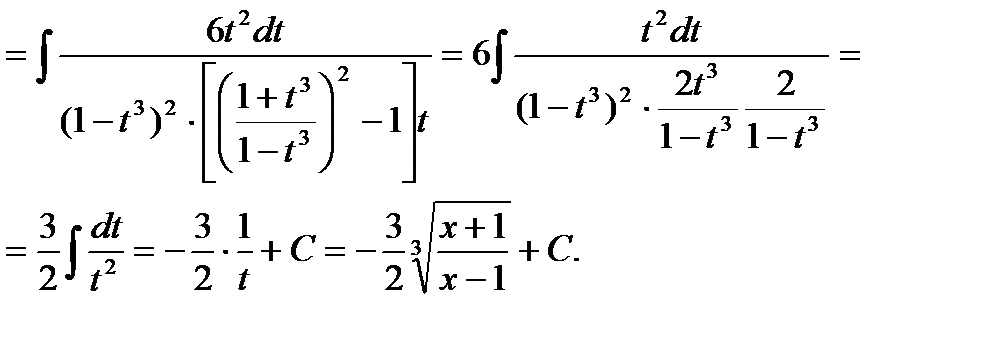
 - многочлен степени n.
- многочлен степени n.
Имеет место следующая формула: 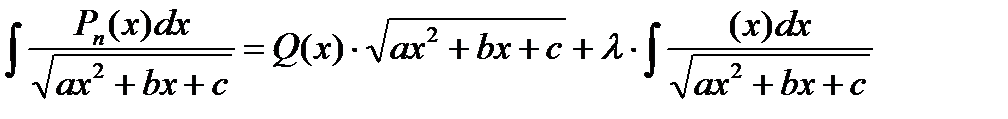
Где 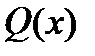 - многочлен степени ”n-1” c неопределенными коэффициентами;
- многочлен степени ”n-1” c неопределенными коэффициентами;
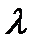 - постоянное число.
- постоянное число.
(доказательство,см.Фихтенг.,т.2,стр.67).
Многочлен 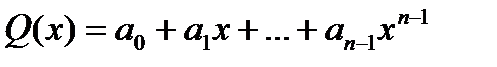 и
и 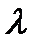 находятся так:
находятся так:
1) Записывают равенство (I) с неопределенными коэффициентами для многочлена Q(x), беря степень многочлена Q(x) на единицу меньше степени многочлена Pn(x).
2) Дифференцируют обе части равенства(I), в результате чего исчезают интегралы.
3) Умножают полученное равенство на 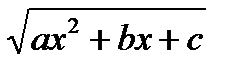 ,в результате чего исчезают иррациональности.
,в результате чего исчезают иррациональности.
4) По методу неопределенных коэффициентов определяют коэффициенты многочлена Q(x) и число 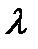 .
.
5) Найденные значения подставляют в формулу и вычисляют интеграл 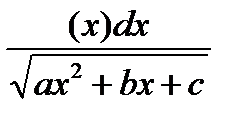
Пример6.6.55.Вычислить 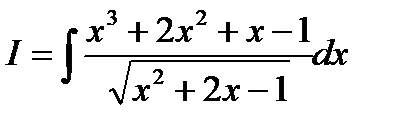 .
.
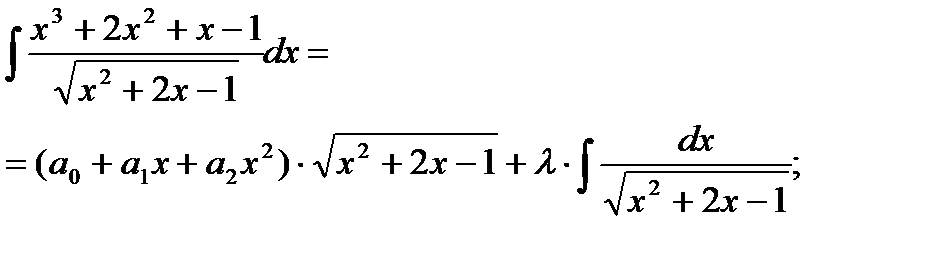
дифференцируем обе части:
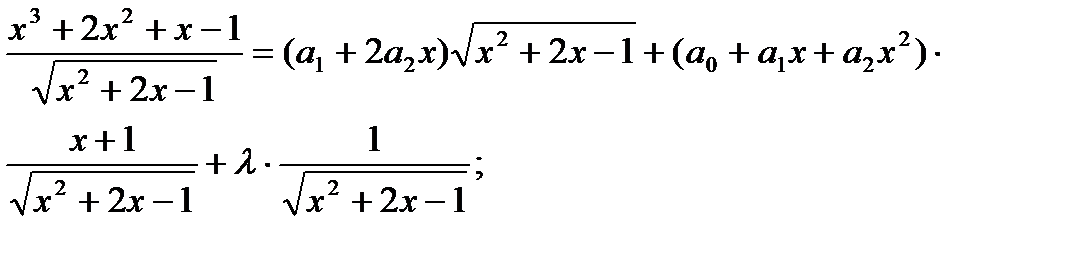
Умножаем почтенно на 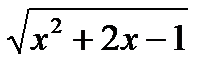 :
:
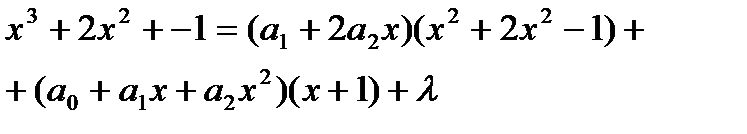 ;
;
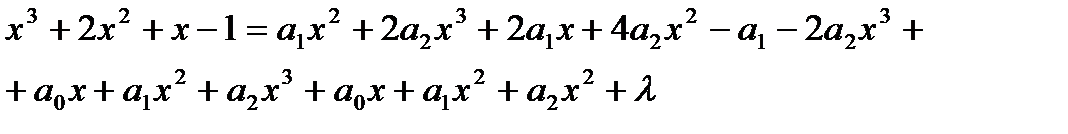
откуда имеем:
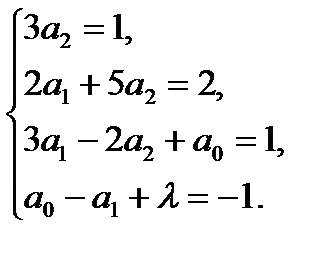
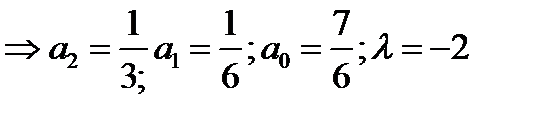
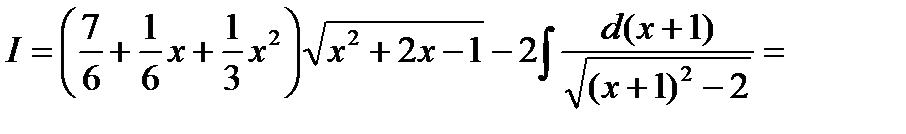
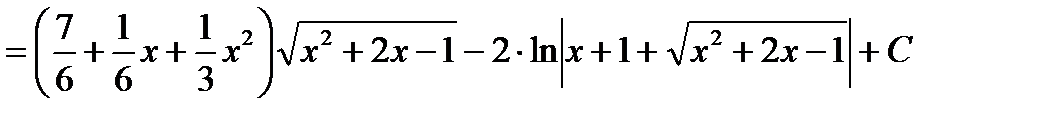
4. 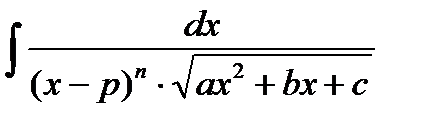 ;где
;где 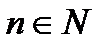
Применяется подстановка 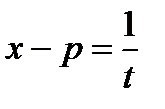 .
.
С помощью этой подстановки интеграл сводится к рассмотренным ранее (в зависимости от “n”).
Пример6.6.56. 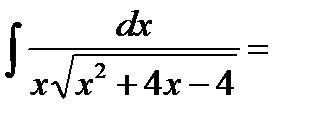
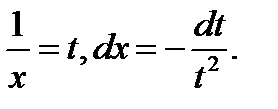
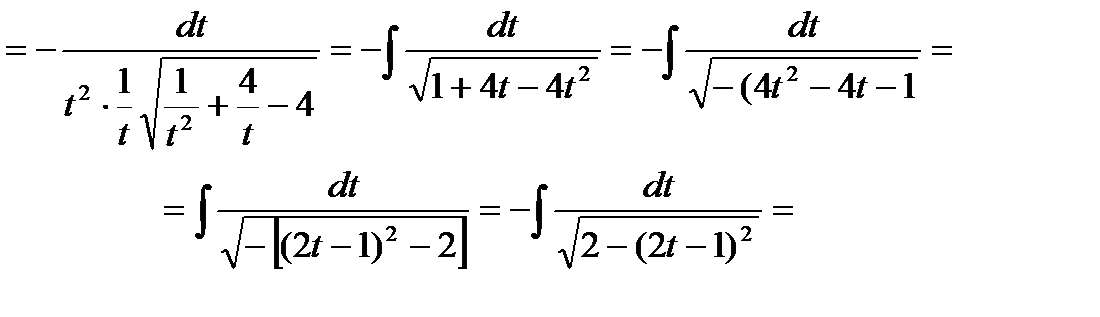
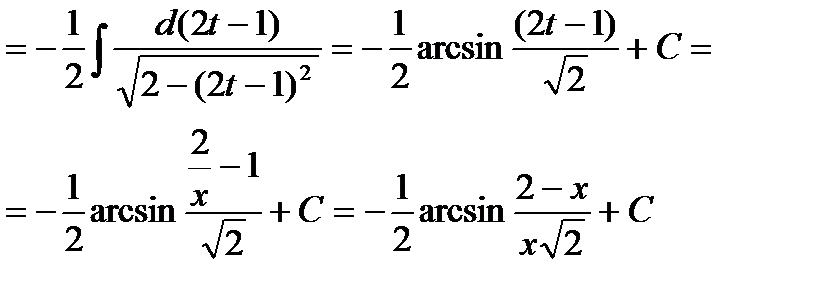 .
.
Дата добавления: 2016-10-17; просмотров: 871;
