Частные подстановки
Как уже было сказано, универсальная подстановка нередко приводит к сложным выкладкам.
В указанных ниже случаях предпочтительнее сделать частные подстановки, так же рационализирующие интеграл:
Если функция 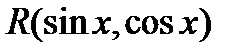 нечетная относительно sinx, т.е.
нечетная относительно sinx, т.е.
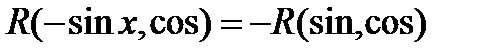 то применима подстановка
то применима подстановка 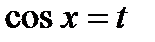
Другими словами, эта подстановка применяется тогда, когда при знаменателе sin на – sinx подынтегральная функция изменяет лишь знак.
Если функция нечетная 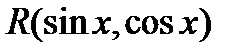 относительно косинуса, т.е.
относительно косинуса, т.е. 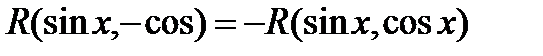 то применима подстановка
то применима подстановка 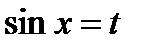
Если функция четная относительно синуса и косинуса, т.е. 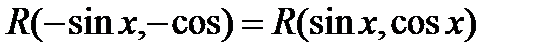 то применима подстановка
то применима подстановка 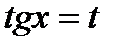
Другими словами, подстановка применяется тогда, когда функция 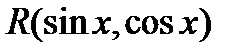 не меняется от перемены знака перед sinx и cosx одновременно
не меняется от перемены знака перед sinx и cosx одновременно
Пример 6.6.36.
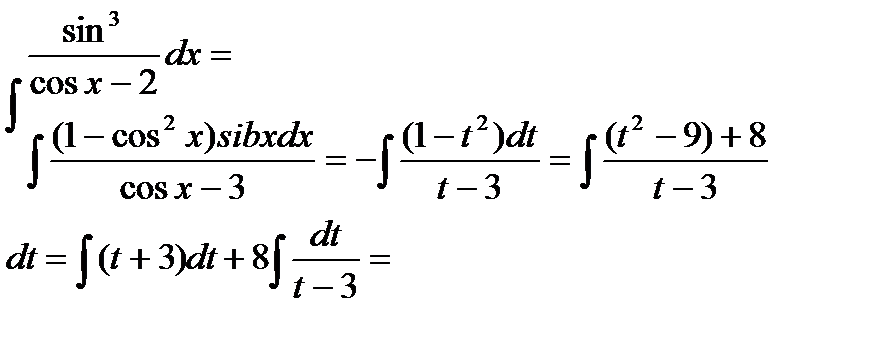
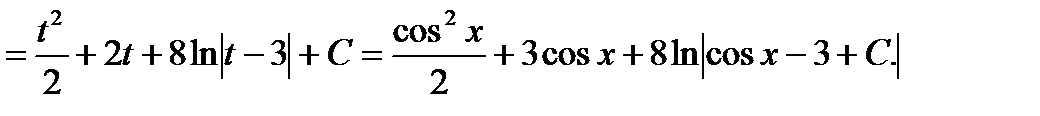 Здесь подынтегральная функция нечетная относительно
Здесь подынтегральная функция нечетная относительно 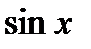 ,поэтому
,поэтому 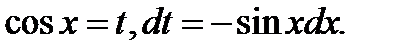
Пример6.6.37.
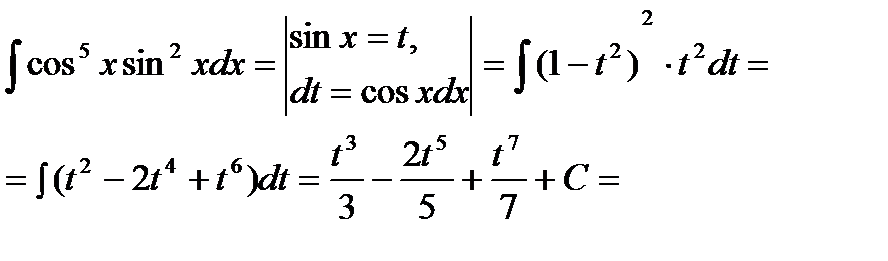
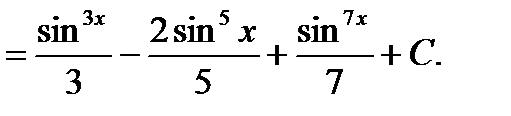 подынтегральная функция нечетна относительно косинуса
подынтегральная функция нечетна относительно косинуса
Пример 6.6.38.
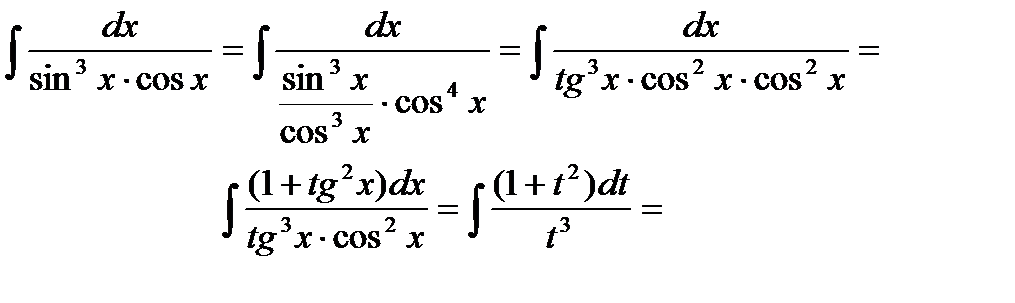
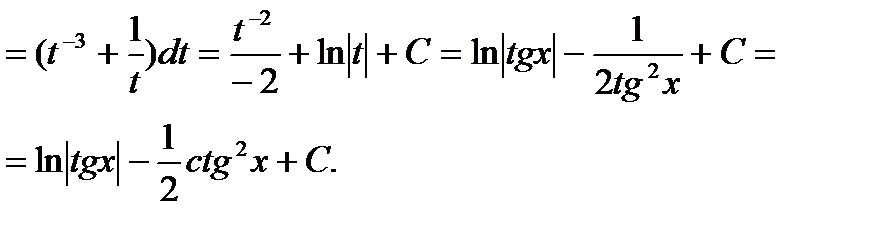
подынтегральная функция четна
относительно синуса. 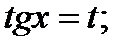
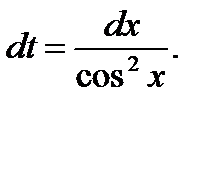
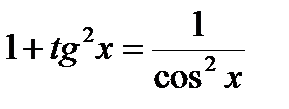
Пример. 6.6.39. 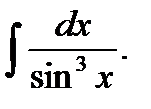
a) подстан. 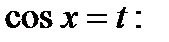
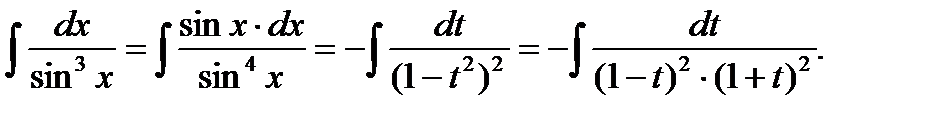
б) подстан. 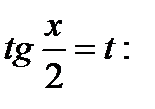
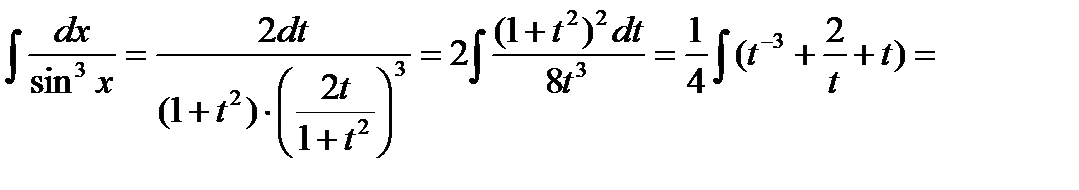
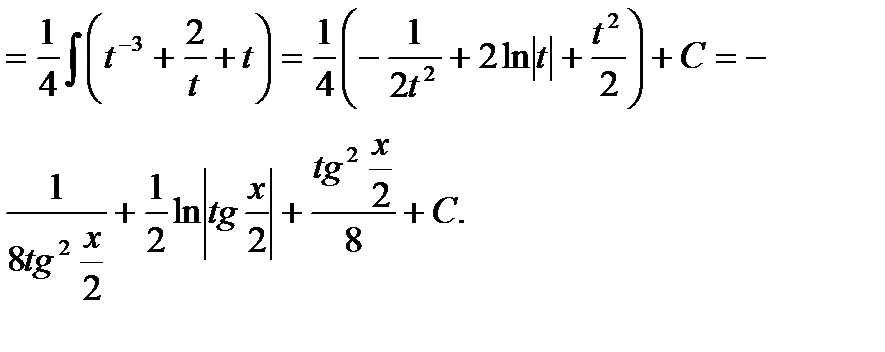
Неопределенные интегралы вида:
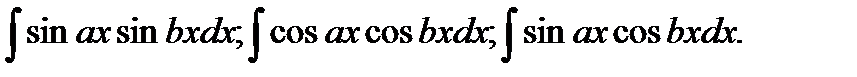
где а и в – простейшие числа; 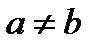
При вычислении таких интегралов необходимо преобразовать произведение тригонометрических функций в сумму или разность, пользуясь одной из следующих формул:
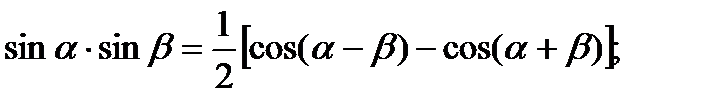
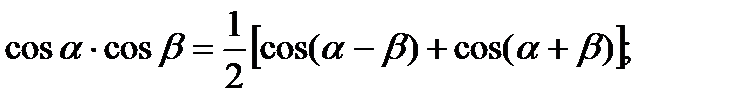
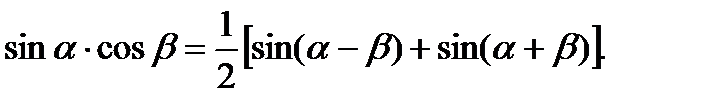
Пример6.6.40. 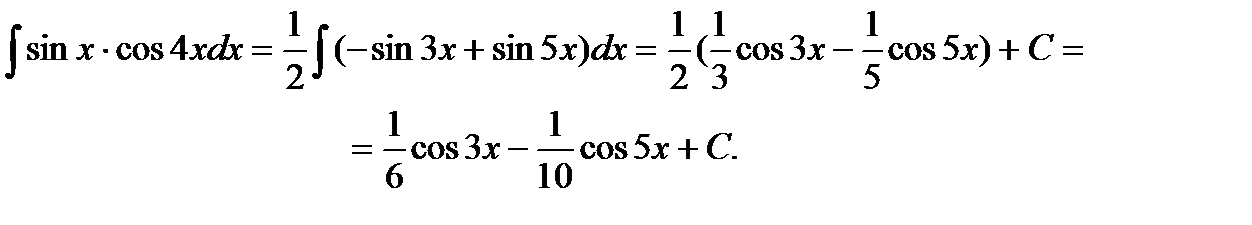
Дата добавления: 2016-10-17; просмотров: 791;
