Интегрирование рациональных дробей
Рациональной дробью называется дробь вида 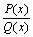 , где P(x) и Q(x) – многочлены. Рациональная дробь называется правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
, где P(x) и Q(x) – многочлены. Рациональная дробь называется правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
Пусть необходимо найти интеграл от неправильной рациональной дроби. При помощи деления (по правилу деления многочленов) неправильную рациональную дробь можно представить в виде суммы целой рациональной функции и правильной рациональной дроби. Например, 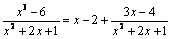 .
.
Затем знаменатель правильной дроби разлагается на множители вида 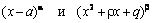 , а правильная дробь разлагается на сумму элементарных дробей следующим образом:
, а правильная дробь разлагается на сумму элементарных дробей следующим образом:
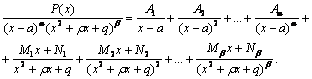
Пример. Найти интеграл 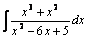 .
.
Решение. Выделим целую часть данной неправильной дроби:
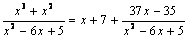 .
.
Разложим знаменатель на линейные множители по формуле: 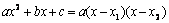 , где х1 и х2 – корни квадратного уравнения
, где х1 и х2 – корни квадратного уравнения 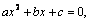 то есть
то есть 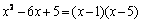 .
.
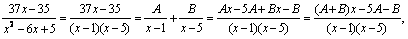
откуда получаем систему уравнений, приравнивая коэффициенты при одинаковых степенях слева и справа 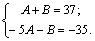
Решая ее, имеем: 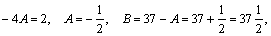 значит:
значит: 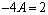 ,
,
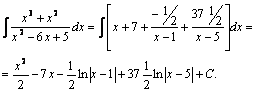
5. Формула Ньютона – Лейбница
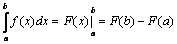 ,
,
где F(x) – первообразная для f(x), т.е. F'(x)=f(x).
Пример.
1. Вычислить 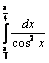 по формуле Ньютона – Лейбница.
по формуле Ньютона – Лейбница.
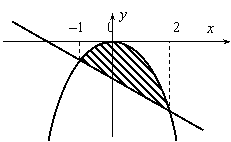 Решение. Имеем
Решение. Имеем 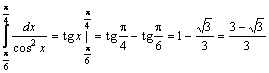 .
.
2. Вычислить 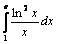 .
.
Решение. Положим 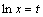 , тогда
, тогда 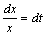 . Если х=1, то t= 0, если х=е, то t= 1. Следовательно,
. Если х=1, то t= 0, если х=е, то t= 1. Следовательно, 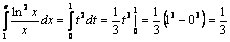 .
.
Дата добавления: 2016-05-11; просмотров: 758;
