Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные дифференциальные уравнения первого порядка
Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+3y=e2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным.
Здесь ρ(x)=3 и f(x)=e2x.
Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значение y и y', получаем: U'υ+Uυ'+3Uυ=e2 x или U'υ+U(υ'+3υ)= e2x.
Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем: 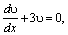
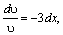 ln υ =–3x,υ=e–3x.
ln υ =–3x,υ=e–3x.
Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
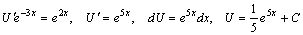 .
.
Итак, общее решение данного уравнения имеет вид:
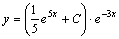 .
.
Найдем частное решение. Для этого подставим начальные условия в выражение для общего решения и найдем С.
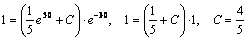 .
.
Частное решение имеет вид: 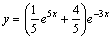 .
.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Рассмотрим линейное уравнение второго порядка вида:
y''+ρy'+qy=0, (1)
у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.
Уравнение
K2+ρK+q=0 (2)
называется характеристическим уравнением данного уравнения (1).
Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.
Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:
1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид 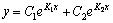 .
.
2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид: 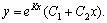
3. Если D<0, то корни характеристического уравнения комплексные: 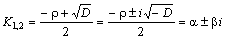 , где
, где 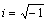 – мнимая единица,
– мнимая единица, 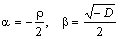 и общее решение (К1=α+βi, К2=α–βi, β≠0), имеет вид y=eαx(C1 cosβx+C2 sinβx).
и общее решение (К1=α+βi, К2=α–βi, β≠0), имеет вид y=eαx(C1 cosβx+C2 sinβx).
Пример 1. Найти общее уравнение y''–y'–2y=0.
Решение. Характеристическое уравнение имеет вид K2–K–2=0, его корни К1=1, К2=–2 вещественные и различные. Общее решение уравнения имеет вид y=C1ex+C2e–2x.
Пример 2. Найти общее решение уравнения y''–2y'+y=0.
Решение. Характеристическое уравнение имеет вид К2–2К+1=0, его корни К1 = К2=1 – вещественные и равные. Общее решение уравнения имеет вид y=ex(C1+C2x).
Пример 3. Найти общее решение уравнения y''–4y'+13y=0.
Решение. Характеристическое уравнение имеет вид К2–4К+13=0, его корни К1=2+3i, К2=2–3i комплексные. Общее решение уравнения имеет вид y=e2x(C1 cos3x+C2sin3x).
Рассмотрим теперь линейное неоднородное уравнение второго порядка:
y''+ρx+qy=f(x), (3)
где f(x) – непрерывная функция, отличная от нуля.
Общее решение такого уравнения представляет собой сумму частного решения 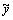 неоднородного уравнения (3) и общего решения yосоответствующего однородного уравнения (1):
неоднородного уравнения (3) и общего решения yосоответствующего однородного уравнения (1):
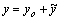 .
.
Поскольку нахождение общего решения однородного уравнения мы уже рассмотрели, то остаются рассмотреть вопрос о нахождении частного решения. Рассмотрим различные виды правых частей уравнения (3).
1) Пусть правая часть имеет вид f(x)=eαxPn(x), где Pn(x) – многочлен степени n. Тогда частное решение 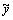 ищем в виде
ищем в виде 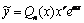 , где Qn(x) – многочлен той же степени, что и Pn(x), а r – число, показывающее, сколько раз α является корнем характеристического уравнения.
, где Qn(x) – многочлен той же степени, что и Pn(x), а r – число, показывающее, сколько раз α является корнем характеристического уравнения.
Пример 4. Найти общее решение уравнения y''–2y'+y=x2+1.
Решение. Общее решение соответствующего однородного уравнения имеет вид yo=ex(C1+C2x )(см. пример 2). Так как правая часть уравнения является многочленом второй степени и ни один из корней характеристического уравнения 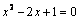 не равен нулю (К1=К2=1), то частное решение ищем в виде
не равен нулю (К1=К2=1), то частное решение ищем в виде 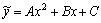 , где А, В, С – неизвестные коэффициенты. Дифференцируя дважды
, где А, В, С – неизвестные коэффициенты. Дифференцируя дважды 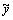 =Ax2+Bx+C и подставляя
=Ax2+Bx+C и подставляя 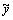 =Ax2+Bx+C,
=Ax2+Bx+C, 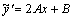 ,
,  в данное уравнение находим 2A–4Ax–2B+Ax2+Bx+C=x2+1, или Ax2+(B–4A)x+2A–2B+C=x2+1.
в данное уравнение находим 2A–4Ax–2B+Ax2+Bx+C=x2+1, или Ax2+(B–4A)x+2A–2B+C=x2+1.
Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства, имеем А=1, В-4А=0, 2А-2В+С=1, Находим А=1, В=4, С=7. Итак, частное решение данного уравнения имеет вид 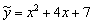 , а общее решение -
, а общее решение - 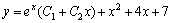 .
.
Пример 5. Найти общее решение уравнения и частное решение, удовлетворяющее начальным условиям
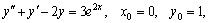
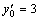 .
.
Решение. Общее решение соответствующего однородного уравнения имеет вид y o=C1ex+C2e–2x (см. пример 1). В правой части данного уравнения стоит произведение многочлена нулевой степени на показательную функцию eαx при α=2. Так как среди корней характеристического уравнения нет корней, равных 2, то частное решение данного уравнения ищем в виде 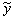 =A∙e2x.
=A∙e2x.
Дифференцируя и подставляя 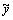 в уравнение получаем:
в уравнение получаем:
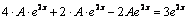 и
и 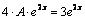 , откуда
, откуда 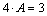 ,
, 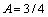 .
.
Подставляя найденное значение А в выражение для 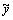 , найдем частное решение данного уравнения
, найдем частное решение данного уравнения 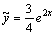 и общее решение запишется в виде
и общее решение запишется в виде 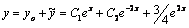 . Найдем частное решение, удовлетворяющее начальным условиям. Для этого продифференцируем у.
. Найдем частное решение, удовлетворяющее начальным условиям. Для этого продифференцируем у. 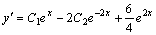 .
.
Подставляем начальные условия в у и у', находим С1 и С2:
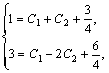
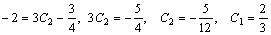 .
.
Подставляя найденное значение С1 и С2 в выражение для у, найдем частное решение данного уравнения
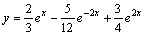 .
.
2) Пусть правая часть имеет вид 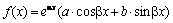 и α+βi, (α–βi) не является корнем характеристического уравнения. Тогда частное решение ищем в виде
и α+βi, (α–βi) не является корнем характеристического уравнения. Тогда частное решение ищем в виде 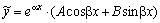 .
.
Если же α+βi, (α–βi) является корнем характеристического уравнения, то частное решение находим в виде 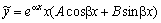 .
.
Пример 6. Найти общее решение уравнения 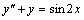 .
.
Решение. Здесь характеристическое уравнение К2+1=0 имеет корни К1= i, К2=-i. Поэтому общее решение соответствующего однородного уравнения будет y=C1cosx+C2sinx. В правой части стоит тригонометрическое функция 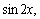 то есть a=0, b=1, β=2. Так как β=2 не является корнем характеристического уравнения, то частное решение надо искать в виде:
то есть a=0, b=1, β=2. Так как β=2 не является корнем характеристического уравнения, то частное решение надо искать в виде: 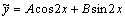 .
.
Дифференцируя 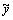 и подставляя его в дифференциальное уравнение, получим
и подставляя его в дифференциальное уравнение, получим 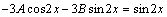 , откуда
, откуда 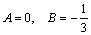 , т.е. частное решение
, т.е. частное решение 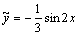 , а общее решение уравнения:
, а общее решение уравнения: 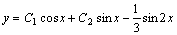 .
.
Интегральное исчисление
1. Первообразная функция и неопределенный интеграл.
Определение. Функция F(x) называется первообразной функцией для функции f(x), если производная ее F'(x)=f(x).
Определение. Совокупность всех первообразных функций F(x)+С для функции f(x) называется неопределенным интегралом функции f(x) и обозначается 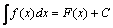 .
.
Таблица основных интегралов:
1. 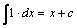 .
.
2. 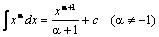 .
.
3. 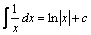 .
.
4. 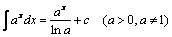 .
.
Следствие:  .
.
5. 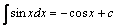 .
.
6. 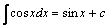 .
.
7. 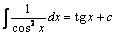 .
.
8. 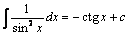 .
.
9. 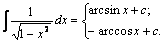
10. 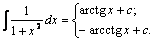
Основные свойства интегралов
1. 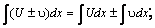
2. 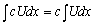
Пример. Вычислить интегралы:
1. 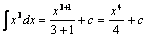 .
.
Проверка. 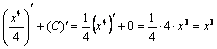 .
.
Дата добавления: 2016-05-11; просмотров: 3419;
