Знакопеременные ряды
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным.
Знакочередующимся называется ряд вида
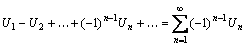 , где
, где 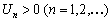 .
.
Ряды вида 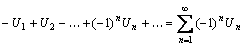 также называются знакочередующимися.
также называются знакочередующимися.
Признак абсолютной сходимости
Знакопеременный ряд
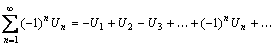 (4)
(4)
сходится, если сходится ряд
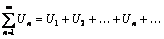 (5)
(5)
Ряд (4) называется в этом случае абсолютно сходящимся. Если ряд (4) сходится, а ряд (5) расходится, то ряд (4) называется условно сходящимся. При этом сходимость ряда (4) можно в ряде случаев установить без исследования ряда (5).
Признак сходимости Лейбница
Пусть имеется знакочередующийся ряд 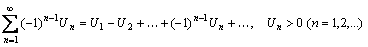 .
.
Если одновременно выполняются следующие два условия:
1) 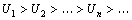 ,
,
2) 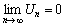 , то такой ряд сходится и его сумма не превосходит первого члена:
, то такой ряд сходится и его сумма не превосходит первого члена: 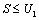 .
.
Степенные ряды
Определение. Ряд вида 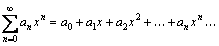 называется степенным рядом. Здесь постоянные величины a1, a2, …, ak,… – коэффициенты ряда, a0 – свободный член. Степенные ряды являются одним из видов функциональных рядов вида
называется степенным рядом. Здесь постоянные величины a1, a2, …, ak,… – коэффициенты ряда, a0 – свободный член. Степенные ряды являются одним из видов функциональных рядов вида
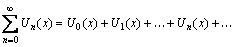 (6)
(6)
Очевидно, любой степенной ряд сходится при х=0. Для любого степенного ряда имеется интервал (–R, R), называемый интервалом сходимости, в каждой точке которого ряд сходится, а вне интервала ряд расходится. На границах интервала ряд может либо сходится, либо расходится. Число R называется радиусом сходимости степенного ряда, он находится по формуле:
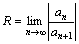 . (7)
. (7)
Таким образом, поиск области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследования сходимости ряда на границах интервала сходимости (при 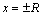 ).
).
Разложение функции f(x) в ряд Маклорена имеет следующий вид: 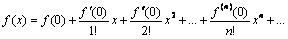 (8)
(8)
Наиболее употребительны разложения следующих функций:
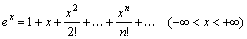 ;
;
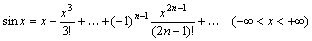 ;
;
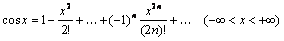 ;
;
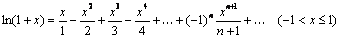 ;
;
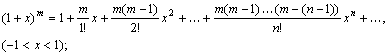
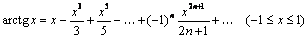 .
.
Пример. Написать три первых члена степенного ряда по заданному общему члену 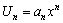 , найти область сходимости ряда
, найти область сходимости ряда 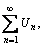 если
если 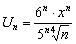 .
.
Решение. Первые три члена ряда будут: 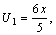
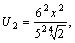
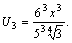
Имеем 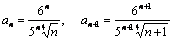 .
.
Определяем радиус сходимости:
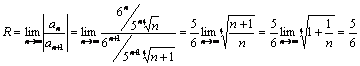 .
.
Интервал сходимости имеет вид: 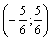 .
.
Пусть 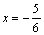 . Получаем числовой ряд:
. Получаем числовой ряд:
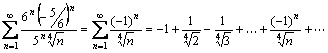 .
.
Применяем к этому знакочередующемуся ряду признак Лейбница:
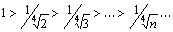 ; (1)
; (1)
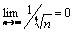 . (2)
. (2)
Оба условия выполняются, следовательно ряд при 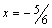 сходится.
сходится.
Пусть 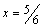 . Имеем числовой ряд:
. Имеем числовой ряд:
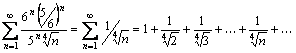 .
.
Сравнивая с расходящимся гармоническим рядом 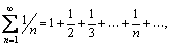 видим, что, начиная с n=2, выполняется- неравенство
видим, что, начиная с n=2, выполняется- неравенство 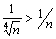 , поэтому по признаку сравнения ряд расходится (так как расходится гармонический ряд). Область сходимости ряда
, поэтому по признаку сравнения ряд расходится (так как расходится гармонический ряд). Область сходимости ряда 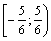 .
.
Пример. Вычислить 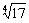 с точностью до 0,0001, используя разложение
с точностью до 0,0001, используя разложение 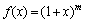 в ряд Маклорена.
в ряд Маклорена.
Решение.
Преобразуем 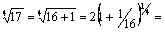

Полученный ряд знакочередующийся и его члены убывают по абсолютной величине, поэтому погрешность не превзойдет первого отброшенного члена.
Очевидно, что 2∙0,00001<0,0001.
Следовательно, 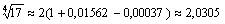 .
.
Дата добавления: 2016-05-11; просмотров: 867;
