ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Определение. Рациональной дробьюназывается отношение двух многочленов:
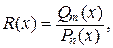 (4)
(4)
где 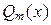 и
и 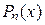 многочлены от
многочлены от 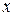 степеней
степеней 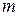 и
и 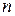 соответственно.
соответственно.
Рациональная дробь (4) называется правильной, если 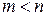 и неправильной, если
и неправильной, если 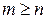 .
.
Определение. Простейшими рациональными дробяминазывают правильные рациональные дроби четырех типов:
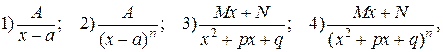
где a, p, q, A, M, N — действительные числа, 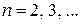
При этом предполагается, что квадратный трехчлен не имеет действительных корней.
Простейшей дроби 1-го и 2-го типов интегрируются заменой 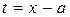 . a 3-го типа — заменой (2). Интегрирование простейших дробей 4-го типа является громоздкими, и мы его рассматривать не будем.
. a 3-го типа — заменой (2). Интегрирование простейших дробей 4-го типа является громоздкими, и мы его рассматривать не будем.
Теорема(о представлении рациональной дроби в виде суммы простейших дробей). Всякую правильную рациональную дробь можно представить, и потом единственным образом, в виде суммы простейших дробей типов 1) — 4). При этом каждому множителю в знаменателе вида 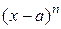 будет соответствовать группа из n слагаемых вида
будет соответствовать группа из n слагаемых вида 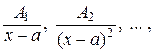
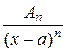 , а каждому множителю в знаменателе вида
, а каждому множителю в знаменателе вида 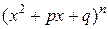 — слагаемые
— слагаемые 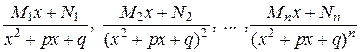 .
.
Постоянные 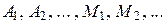 , N1, N2, … называют неопределенными коэффициентами и находят по следующему алгоритму:
, N1, N2, … называют неопределенными коэффициентами и находят по следующему алгоритму:
1) Сумму всех простейших дробей привести к общему знаменателю, который равен знаменателю дроби в левой части тождества.
2) Числитель получившейся дроби приравнять к числителю исходной дроби.
3) Приравнять коэффициенты при одинаковых степенях 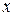 многочленов в левой и правой частях полученного тождества.
многочленов в левой и правой частях полученного тождества.
4) Решить полученную систему уравнений, которая имеет единственное решение.
Теорема(о представлении неправильной рациональной дроби в виде суммы многочлена и правильной дроби). Всякую неправильную рациональную дробь 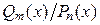
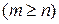 можно разложить, и притом единственным образом, на сумму многочлена
можно разложить, и притом единственным образом, на сумму многочлена 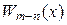 (целая часть) и правильной рациональной дроби
(целая часть) и правильной рациональной дроби 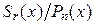
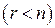 (
( 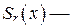 «остаток» от деления
«остаток» от деления 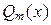 на
на 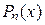 ):
):
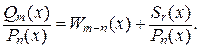
Итак, алгоритм интегрирования рациональных дробей:
1) Если подынтегральная дробь неправильная, то из неё выделяют целую часть 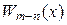 , которая интегрируется непосредственно, и правильную рациональную дробь
, которая интегрируется непосредственно, и правильную рациональную дробь 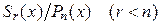 .
.
2) Правильную рациональную дробь 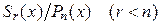 раскладывают на сумму простейших дробей 1) — 4).
раскладывают на сумму простейших дробей 1) — 4).
3) Простейшие дроби интегрируют по отдельности с помощью соответствующих замен переменных.
Пример.Найти интегралы от рациональных дробей.
а)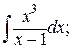 б)
б) 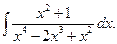
Решение.
а) Подынтегральная дробь неправильная, поэтому выделим целую часть путем деления многочлена на многочлен «углом»:

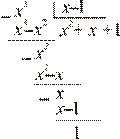
Итак, 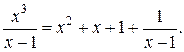
Тогда
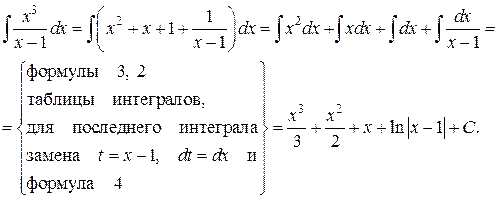
б) Подынтегральная дробь правильная, знаменатель это дроби разложим на множители, а затем разложим дробь на сумму простейших дробей:
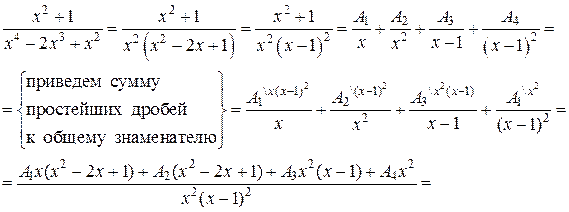
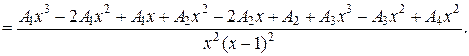
Итак, получим
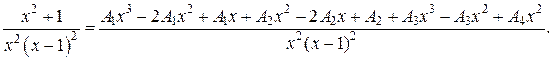
Поскольку знаменатели исходной и полученной дробей одинаковы, то приравняем их числители и получим тождество
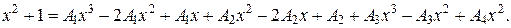
Сгруппируем в правой части слагаемые с одинаковыми степенями, а затем приравняем коэффициенты при одинаковых степенях x в левой и правой частях:
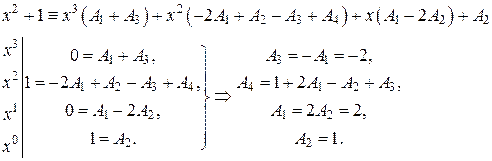
Следовательно, разложение имеет вид:
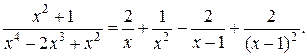
Вернемся к вычислению интеграла:
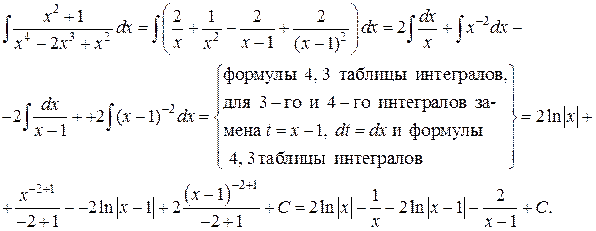
Дата добавления: 2016-09-20; просмотров: 1180;
