ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Определенный интеграл широко используется в различных приложениях, например, при вычислении площадей плоских фигур, длин дуг плоских кривых, объемов тел вращения, площадей поверхностей вращения, работы переменной силы на отрезке, пути, пройденного за промежуток времени, статических моментов и моментов инерции плоских дуг и фигур и т. д.
Площади плоских фигур
Вычисление площадей плоских фигур в декартовой системе координат
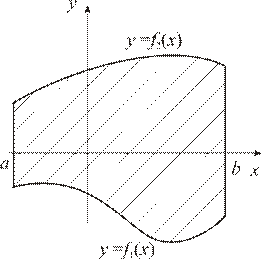
Теорема. Если плоская фигура (рис. 1) ограничена линиями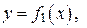 
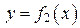, где 
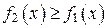для всех 
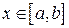, и прямыми 
, 
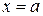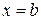, то ее площадь вычисляется по формуле:
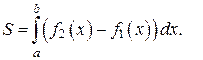(11)
| 
|
| Рис. 1 | Рис. 2 |
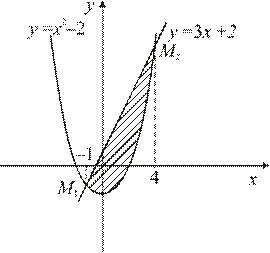
Пример.Найти площадь фигуры, ограниченной линиями:
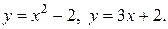
Решение. Построим схематический рисунок (рис. 2). Для построения параболы возьмем несколько точек:
| x | –1 | –2 | –3 | –4 | |||||
| y | –2 | –1 | –1 |
Для построения прямой достаточно двух точек, например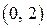 
и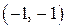 
.
Найдем координаты точек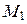 
и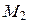 
пересечения параболы 
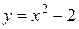и прямой 
.
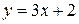Для этого решим систему уравнений
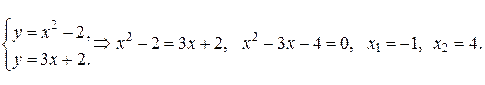
Тогда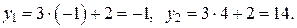 
Итак,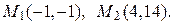 
Площадь полученной фигуры найдем по формуле (11), в которой
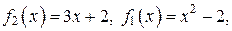поскольку 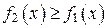для всех 
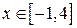. Получим:
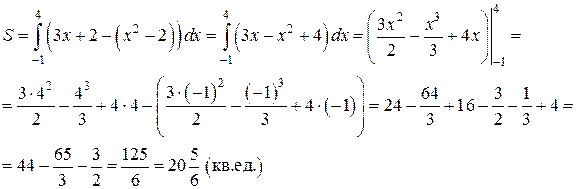
Вычисление площадей фигур, ограниченных линиями, заданными
Параметрически
Теорема. Если функци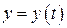и 
и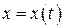 
имеют непрерывные производные первого порядка для всех 
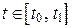, то площадь плоской фигуры, ограниченной линией 
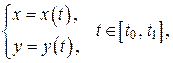прямыми x = a, x = b, где a = x(t0), b = x(t1), и осью OX, вычисляется по формуле:
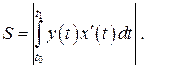(12)
Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически:
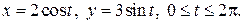
Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра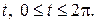 
| t |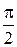 
| 
| 
| 
| |
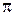
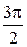
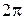
| x | –2 | ||||
| y | –3 |
|
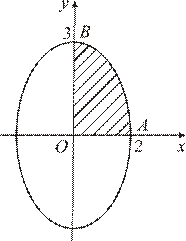
| Рис. 3 |
Нанесем точки (x, y) на координатную плоскость XOY и соединим плавной линией. Когда параметр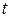 
изменяется от 
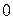до 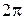, соответствующая точка 
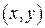описывает эллипс (известно, что 
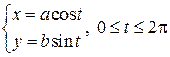— параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдем её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим:
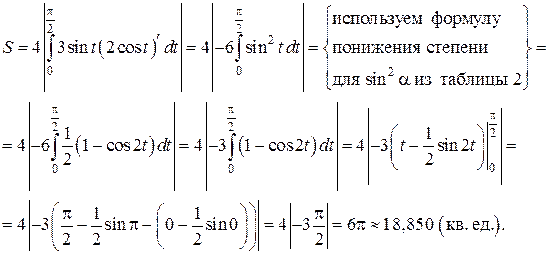
Заметим, что для вычисления площади по формуле (9), построение чертежа не является обязательным, а носит иллюстративный характер.
Дата добавления: 2016-09-20; просмотров: 734;