ПРИБЛИЖЁННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ

Пусть требуется вычислить 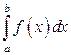, где функция 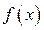непрерывна на отрезке 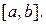Точками 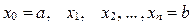разобьём отрезок 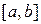на n равных частей, длина каждой из которых равна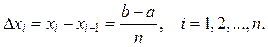

Обозначим 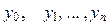значения функции 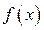в точках разбиения.

Метод прямоугольников

Учитывая геометрический смысл определённого интеграла и заменяя приближённо площади маленьких криволинейных трапеций площадями соответствующих прямоугольников, получим:

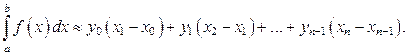
Поскольку все отрезки одинаковой длины, то окончательно имеем:

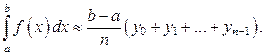(17)

Формула (17) называется формулой левых прямоугольников для приближённого вычисления определённого интеграла. Выбирая прямоугольники другим способом, получим формулу правых прямоугольников:

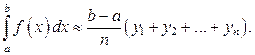(18)

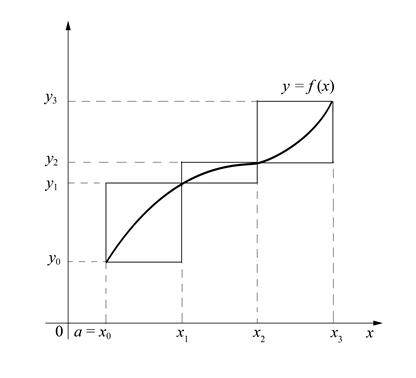
Чем больше число разбиений n, тем точнее приближённое значение определённого интеграла, вычисленного по формулам (17) и (18).

Чтобы оценить найденное приближённое значение определённого интеграла число n отрезков разбиения увеличивают в два раза и сравнивают полученные значения интегралов и оставляют первые совпадающие знаки, если точность недостаточна, то снова удваивают число разбиений.

Отметим, что погрешность R формул прямоугольников оценивается формулой: 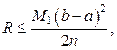где М₁ – верхняя граница модуля первой производной функции на отрезке 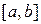, т.е.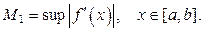

Метод трапеций

Каждую маленькую криволинейную трапецию приближённо заменим линейной трапецией, площадь которой 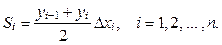Тогда

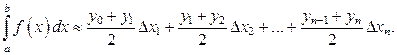
Поскольку все отрезки одинаковой длины, то окончательно имеем:

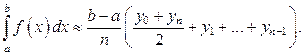(19)

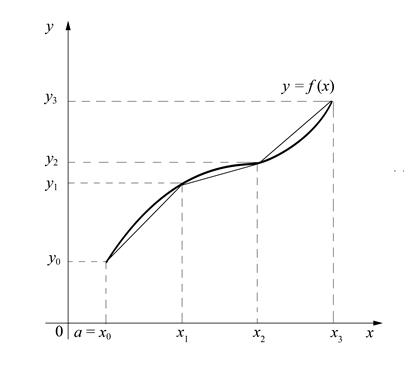
Формула (19) называется формулой трапеций для приближённого вычисления определённого интеграла. Для погрешности R формулы (19) cпра-ведлива оценка 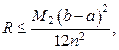где М₂ – верхняя граница модуля второй производной функции на отрезке 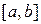, т.е.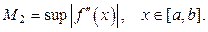

Мы привели только два метода приближённого вычисления определённого интеграла, существует и другие численные методы вычисления определённых интегралов, учитывающих особенности подынтегральных функций.