Длина дуги плоской кривой

Вычисление дуги плоской кривой в декартовых координатах

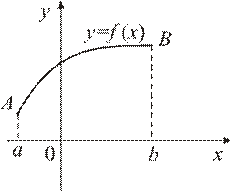
Рис. 4

Если кривая задана уравнением 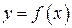, функция имеет непрерывную первую производную при всех , то длина дуги 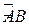(рис. 4) этой кривой, заключенной между точкам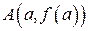и и 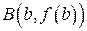, вычисляется по формуле:

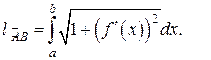(13)

Вычисление длины дуги кривой, заданной параметрически

Если кривая задана параметрически 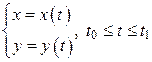, и функции 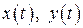имеют непрерывные производные 1-го порядка при всех 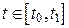, то длина дуги 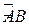, соответствующей изменению параметра от 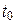до 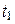, вычисляется по формуле:

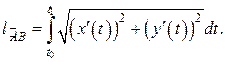(14)

Пример. Найти длину дуги кривой

а) 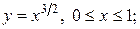б)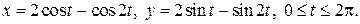

Решение.

а) Так как кривая задана в декартовой системе координат уравнением

, то для вычисления длины дуги воспользуемся формулой (13). Най-

дем :

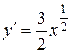и подставим в (13):

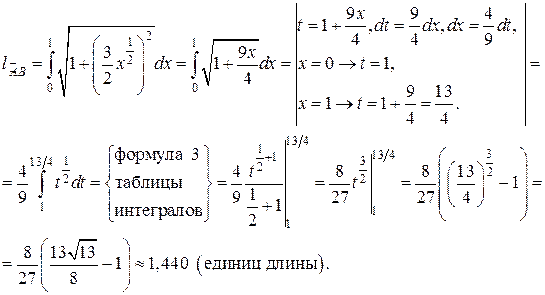
б)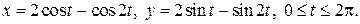

Кривая задана параметрически, поэтому воспользуемся формулой (14). Найдем :

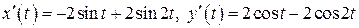и подставим в (14):

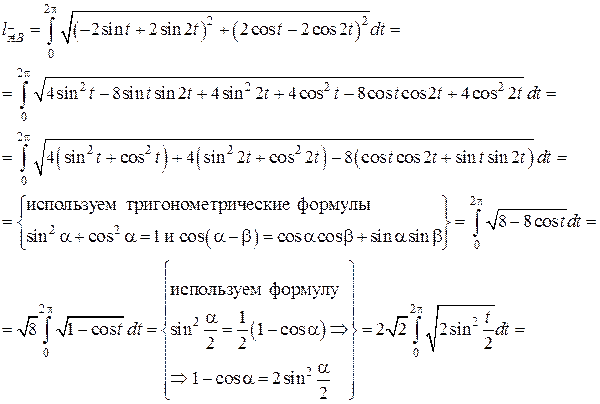
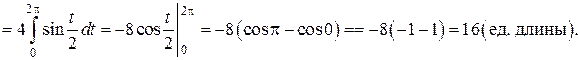Вычисление объемов тел вращения

Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой 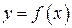, осью OX и прямыми 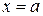, 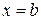(рис. 5), то его объем вычисляется по формуле:

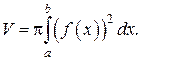(15)

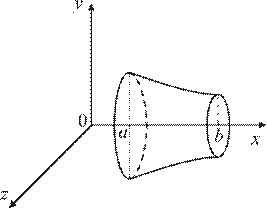
Рис. 5	Рис. 6

Пример. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: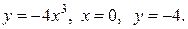

Решение. Построим криволинейную трапецию, вращением которой получается тело вращения (рис. 6).

Чтобы получить объем тела вращения из объема 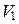тела, полученного вращением фигуры ОАВС, вычтем объем 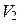тела, полученного вращением фигуры ОАВ. Тогда искомый объем 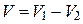. По формуле (15) найдем 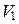и 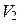: 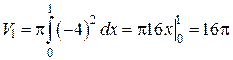(ед. объема);

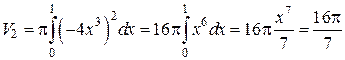(ед. объема);

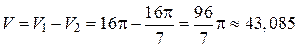(ед. объема).