ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Рассмотрим некоторые из интегралов от тригонометрических функций. Виды интегралов и способы их вычисления приведем в таблице 2.
Таблица 2.
| Вид интеграла | Метод интегрирования |
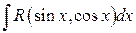 Общий случай
Общий случай
| Замена 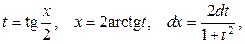
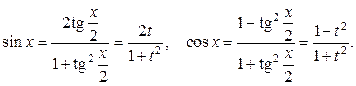
|
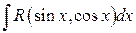 , где , где
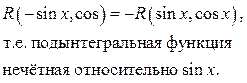
| Замена 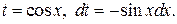
|
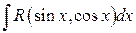 , где , где
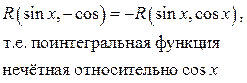
| Замена 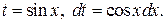
|
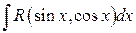 , где , где
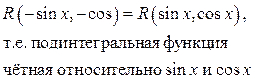
| Замена 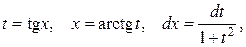
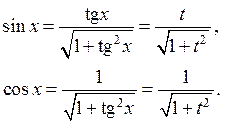
|
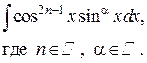
| Замена 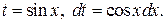 Если
Если 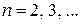 , то необходимо учитывать формулу , то необходимо учитывать формулу 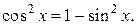
|
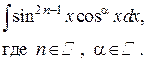
| Замена 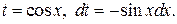 Если
Если 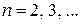 , то необходимо учитывать формулу , то необходимо учитывать формулу 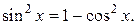
|

| Использовать формулы понижения степени:
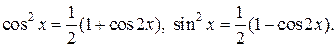
|
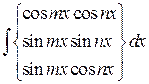
| Использовать формулы преобразования произведения тригонометрических функций в сумму:
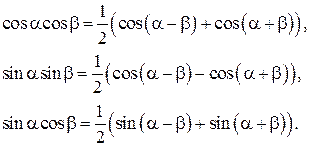
|
Пример. Найти интегралы:
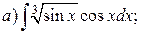
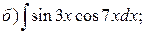
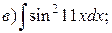
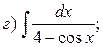
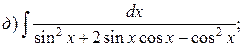
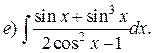
Решение.
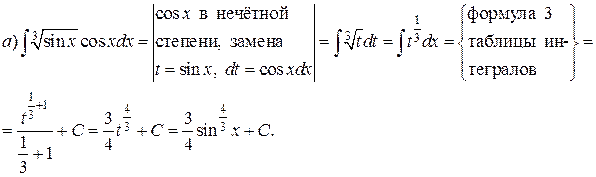
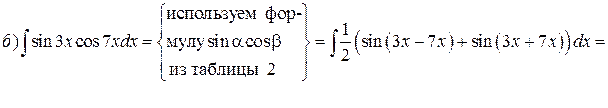
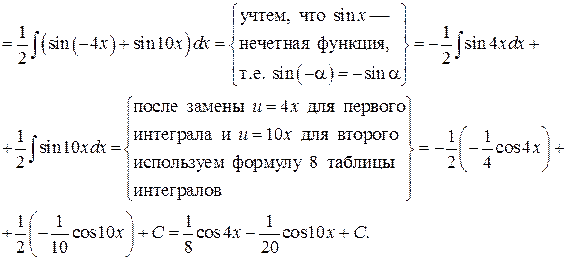
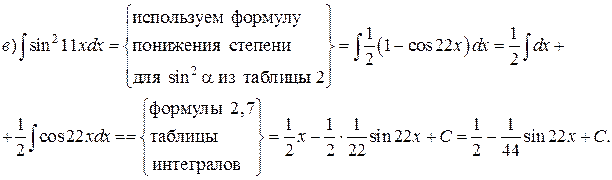
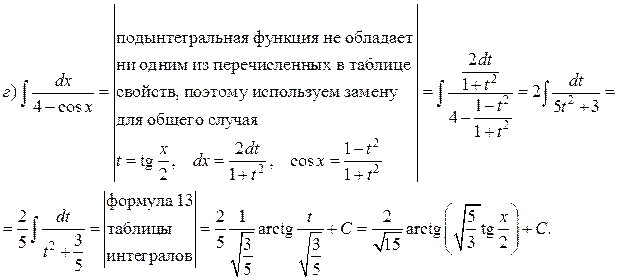
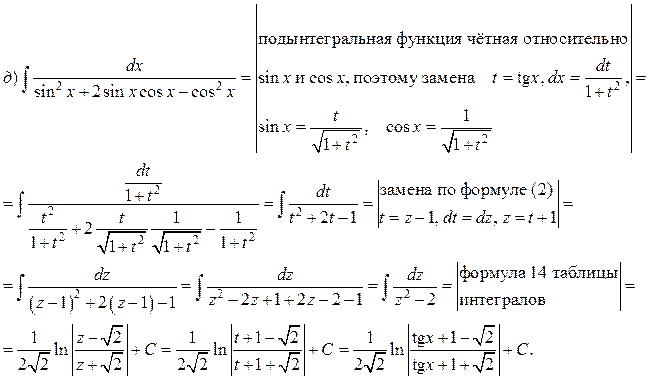
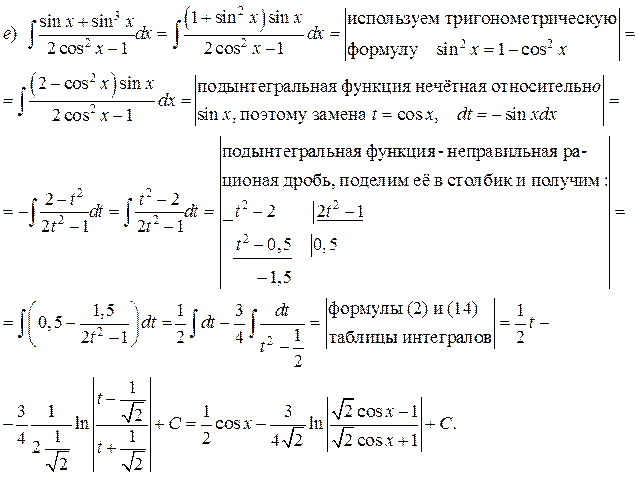
ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ ИРРАЦИОНАЛЬНЫХ
ФУНКЦИЙ
Определение. Иррациональностью от 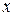 называют выражение, содержащее переменную
называют выражение, содержащее переменную 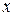 в дробной степени.
в дробной степени.
Рассмотрим интеграл
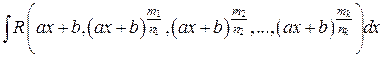 ,
,
где R — рациональная функция; m1, n1, m2, n2, . . . — целые числа.
Подстановка, рационализирующая подынтегральную функцию, имеет вид:
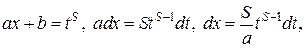
где S — наименьшее общее кратное (НОК) чисел 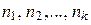 , т. е. наименьшее натуральное число, делящееся нацело на
, т. е. наименьшее натуральное число, делящееся нацело на 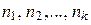 .
.
Пример.Проинтегрировать иррациональность .
Решение.
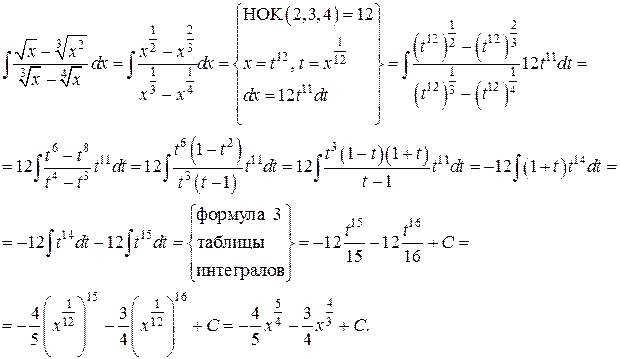
Дата добавления: 2016-09-20; просмотров: 724;
