НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Определение. Функция 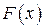 , определенная на интервале
, определенная на интервале 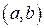 , называется первообразной для функции
, называется первообразной для функции 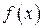 , определенной на том же интервале
, определенной на том же интервале 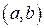 , если
, если 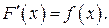
Теорема (о первообразной для данной функции). Если 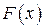 — первообразная для функции
— первообразная для функции 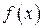 , то любая другая первообразная
, то любая другая первообразная 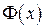 для функции
для функции 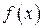 отличается от
отличается от 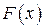 на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е. 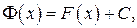 где
где 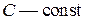 .
.
Доказательство. 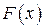 — первообразная для функции
— первообразная для функции 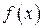 , т.е.,
, т.е., 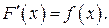
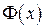 — другая первообразная для
— другая первообразная для 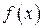 , т.е.,
, т.е., 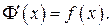 Согласно следствию 3 из теоремы Лагранжа, если производные функций равны друг другу, то разность этих функций равна постоянной С:
Согласно следствию 3 из теоремы Лагранжа, если производные функций равны друг другу, то разность этих функций равна постоянной С: 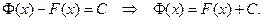
Следствие. Если 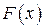 — любая первообразная для функции
— любая первообразная для функции 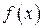 , то всю совокупность первообразных для этой функции определяет выражение
, то всю совокупность первообразных для этой функции определяет выражение 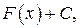 где
где 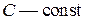 .
.
Определение. Неопределенным интегралом от функции 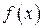 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 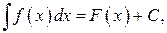 где
где 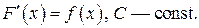 При этом х называется переменной интегрирования,
При этом х называется переменной интегрирования, 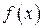 — подынтегральной функцией, а
— подынтегральной функцией, а 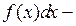 подынтегральным выражением.
подынтегральным выражением.
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию. Результат интегрирования можно проверить дифференцированием.
Определение. График функции 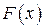 , являющейся первообразной для
, являющейся первообразной для 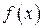 , называется интегральной кривой.
, называется интегральной кривой.
Геометрический смысл неопределённого интеграла состоит в том, что он представляет собой совокупность всех интегральных кривых. График совокупности можно получить из графика одной интегральной кривой, если его перемещать параллельно самому себе вдоль оси ОY.
Свойства неопределенного интеграла:
1. 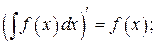
Доказательство: 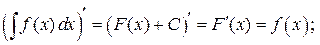
2. 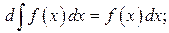
Доказательство: 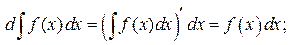
3. 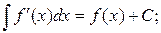
4. 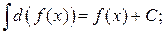
5. 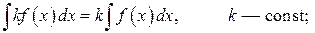
6. 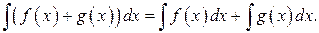
Свойство 6 справедливо для любого конечного числа слагаемых.
Объединяя свойства 5 и 6, получаем свойство линейности неопределённого интеграла.
7. 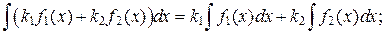
8. Теорема (об инвариантности формул интегрирования). Если 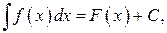 то
то 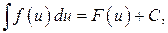 где
где 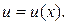
Доказательство: Так как дифференциал первого порядка обладает свойством инвариантности, то 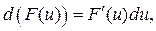 где
где 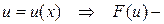 первообразная для
первообразная для 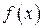 , а значит
, а значит 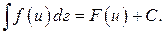
Поскольку операции интегрирования и дифференцирования обратны друг другу, то таблица основных интегралов легко получается из таблицы производных. Приведём таблицу основных интегралов для функции 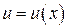 . При этом вместо буквы u при интегрировании может быть использована любая буква, например x, t, z и т. д. Кроме формул, получающихся непосредственно из таблицы производных, в таблицу интегралов включено несколько часто встречающихся интегралов.
. При этом вместо буквы u при интегрировании может быть использована любая буква, например x, t, z и т. д. Кроме формул, получающихся непосредственно из таблицы производных, в таблицу интегралов включено несколько часто встречающихся интегралов.
Таблица основных интегралов
1. 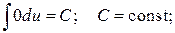 2.
2. 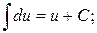
3. 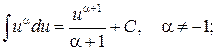
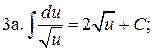
4. 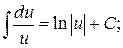 5.
5. 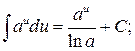
6. 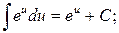 7.
7. 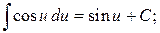
8. 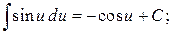 9.
9. 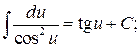
10. 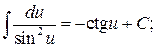 11.
11. 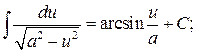
12. 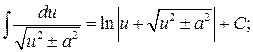 13.
13. 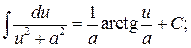
14. 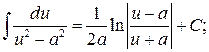 15.
15. 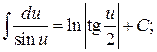
16. 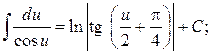 17.
17. 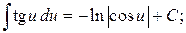
18. 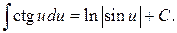
Пример. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы:
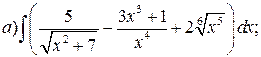
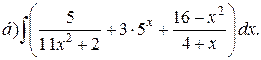
Решение.
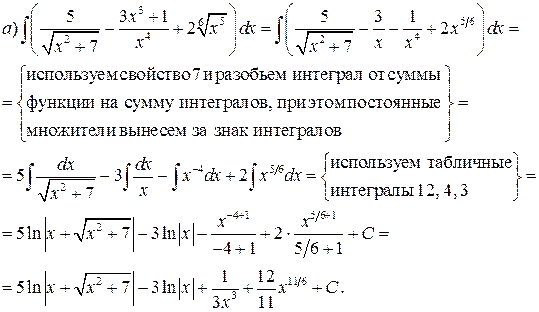
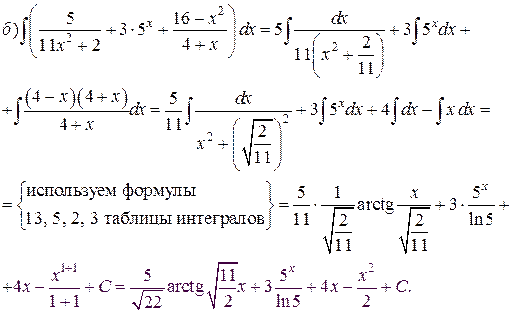
Дата добавления: 2016-09-20; просмотров: 1621;
