НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Определение.Несобственными интегралами называются интегралы с бесконечными пределами (несобственные интегралы 1-го рода) и интегралы от неограниченных функций (несобственные интегралы 2-го рода).

Пусть функция 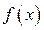определена и непрерывна на полусегменте 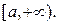Возьмём любое 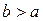и рассмотрим интеграл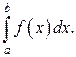

Определение. Если существует конечный предел 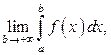то этот предел называется несобственным интегралом от функции 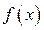на интервале 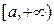и обозначается 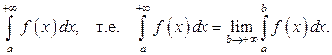Говорят, что в этом случае несобственный интеграл существует или сходится. Если при 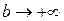интеграл 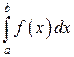не имеет конечного предела, то говорят, что интеграл 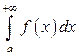не существует или расходится.

Геометрический смысл несобственного интеграла 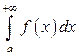состоит в том, что при 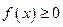для всех 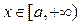он выражает площадь неограниченной области, заключённой между линиями 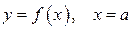и осью ОХ.

Аналогично определяются несобственные интегралы на интервалах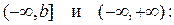

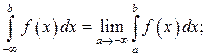
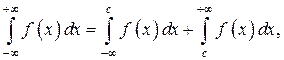где с – любая точка на интервале

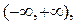причём 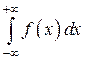существует, если сходятся оба интеграла в пра

вой части и расходится, если расходится хотя бы один из них.

Рассмотрим, как вычисляются несобственные интегралы 1-го рода.

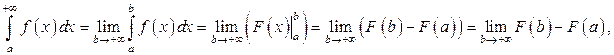
где 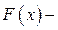первообразная для 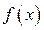, т.е.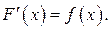

Аналогично 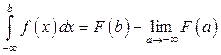и

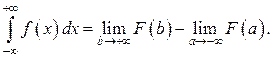
Пример.Вычислить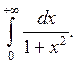

Решение.

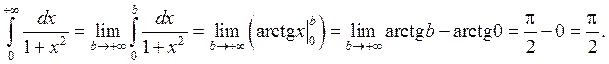
Рассмотрим несобственные интегралы 2-го рода. Пусть функция 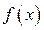имеет бесконечный разрыв в точке 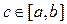и непрерывна пр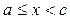и и 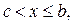тогда полагают, что несобственный интеграл определяется формулой:

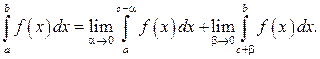(16)

При этом несобственный интеграл называется сходящимся, если существуют оба предела в правой части равенства и расходящимся, если не существует хотя бы один из них.

Геометрический смысл несобственного интеграла 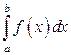состоит в том, что при 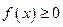для всех 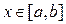он выражает площадь неограниченной области, заключённой между линиями 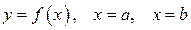и осью ОХ.

Пример.Исследовать на сходимость интеграл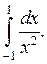

Решение.Интеграл 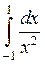является несобственным интегралом 2-го

рода, так как промежуток интегрирования содержит точку бесконечного разрыва 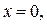поэтому согласно формуле (16):

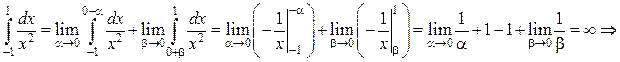
несобственный интеграл расходится.