Задание 8. Вычислить поверхностные интегралы
Второго рода
8.1 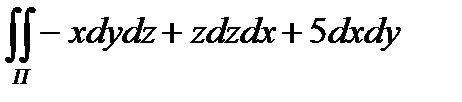 по верхней стороне
по верхней стороне
части плоскости 2x + 3y + z = 6 лежащей в 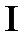 октанте
октанте
8.2 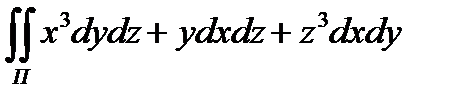 по положительной
по положительной
стороне куба , составленного плоскостями x = 0 ,
y = 0 ,z = 0 , x =1, y =1 , z =1
8.3 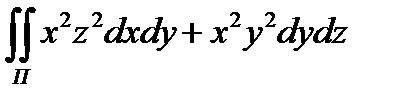 по внешней стороне
по внешней стороне
поверхности , составленной плоскостями x = 0 , y =0
z = 0 ,x + y + z = 1
8.4 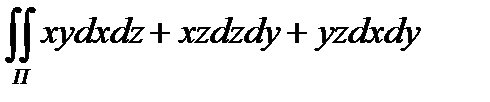 по внешней
по внешней
поверхности , расположенной в 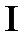 октанте и
октанте и
составленной из плоскостей x = 0 , y =0 , z =0 , z = h
и цилиндра x 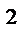 + y
+ y 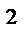 =R
=R 
8.5 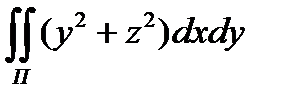 по верхней стороне части
по верхней стороне части
поверхности z = 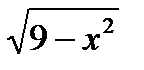 , отсеченной плоскостями
, отсеченной плоскостями
y = 0 ,y =2
8.6 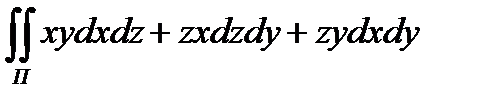 по положительной
по положительной
стороне куба , составленного плоскостями x = 0 ,
y = 0 ,z = 0 , x =1, y =1 , z =1
8.7 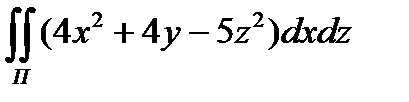 по внутренней стороне
по внутренней стороне
части поверхности x 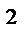 = 4y , отсеченной
= 4y , отсеченной
плоскостями y = 4 , z = 0 , z = 3
8.8 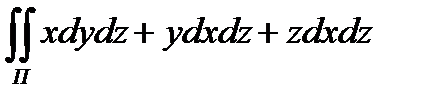 по положительной
по положительной
стороне куба , образованного плоскостями x =0 ,
y = 0 ,z = 0 , x =3 , y = 3 , z = 3
8.9 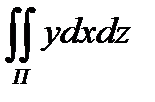 по верхней стороне части плоскости
по верхней стороне части плоскости
x + y + z = a , лежащей в 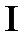 октанте
октанте
8.10 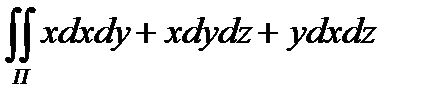 по верхней стороне
по верхней стороне
треугольника , образованного пересечением
плоскости x + y + z =1 cкоординатными
плоскостями
8.11 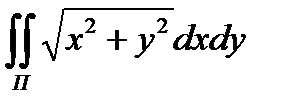 по нижней стороне круга
по нижней стороне круга
x 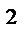 + y
+ y 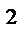
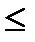 R
R 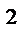
8.12 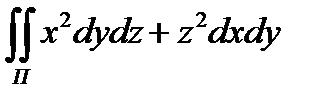 по нижней стороне части конуса x
по нижней стороне части конуса x 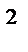 + y
+ y 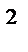 = z
= z 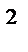 , 0
, 0 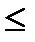 z
z 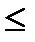 1
1
8.13 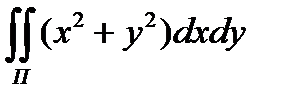 по нижней стороне круга
по нижней стороне круга
x 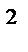 + y
+ y 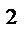 = R
= R 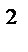
8.14 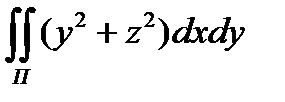 по верхней стороне цилиндрической поверхности z
по верхней стороне цилиндрической поверхности z 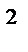 = 1 - x
= 1 - x 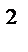 , 0
, 0 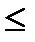 y
y 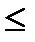 1
1
8.15 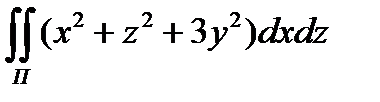 по внешней стороне части
по внешней стороне части
Дата добавления: 2016-10-17; просмотров: 890;
