Схема исследования функции на экстремумы
1. Найти производную 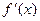 .
.
2. Найти критические точки функции, в которых производная 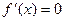 или не существует.
или не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4. Вычислить значения функции в точках экстремума.
ПримерНайти экстремумы функции f(x) = 2x3 - 15x2+ 36x - 14.
Решение. Так как f ¢ (x) = 6x2 - 30x +36 = 6(x -2)(x - 3), то критические точки функции x1 = 2 и x2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x2 = 3 производная меняет знак минус на плюс, поэтому в точке x2 = 3 у функции минимум. Вычислив значения функции в точках x1 = 2 и x2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Пусть функция 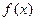 дифференцируема на интервале (a, b).
дифференцируема на интервале (a, b).
Функция 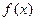 выпукла (вогнута) на интервале (а, в) если в пределах этого интервала график функции лежит не выше (ниже) любой своей касательной.
выпукла (вогнута) на интервале (а, в) если в пределах этого интервала график функции лежит не выше (ниже) любой своей касательной.
Теорема:Пусть функция 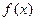 определена на интервале (а, в) и
определена на интервале (а, в) и 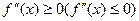 ,
, 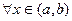 , тогда
, тогда 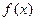 выпукла вниз (выпукла вверх) на интервале (а,b). Если неравенство
выпукла вниз (выпукла вверх) на интервале (а,b). Если неравенство 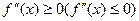 строгое, то
строгое, то 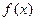 строго выпукла вверх (строго выпукла вниз).
строго выпукла вверх (строго выпукла вниз).
Точки перегиба
Точка графика дифференцируемой функции 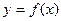 , при переходе через которую график меняет выпуклость на вогнутость и наоборот называется точкой перегиба.
, при переходе через которую график меняет выпуклость на вогнутость и наоборот называется точкой перегиба.
Теорема 1 (Достаточное условие перегиба):Вторая производная 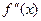 обращается в точке х0 функции
обращается в точке х0 функции 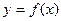 обращается в ноль и при переходе через эту точку меняет знак, то точка с координатами (х0,f(x0)) графика данной функции является точкой перегиба.
обращается в ноль и при переходе через эту точку меняет знак, то точка с координатами (х0,f(x0)) графика данной функции является точкой перегиба.
Теорема 2 (Необходимое условие перегиба):Вторая производная 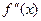 дважды дифференцируемой функции в точке перегиба равна нулю, то есть
дважды дифференцируемой функции в точке перегиба равна нулю, то есть 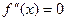 .
.
Дата добавления: 2016-06-24; просмотров: 3836;
