Общая схема исследования функции и построения ее графика.
1. Найти область определения функции.
2. Исследовать на четность и нечетность.
3. Найти точки пересечения с осями.
4. Найти промежутки монотонности и точки экстремума.
5. Исследовать функцию на выпуклость и вогнутость. Найти точки перегиба.
6. Найти асимптоты графика функции.
7. Найти некоторые дополнительные точки (при необходимости)
8. Построить график функции.
Лекция 9 Интегральное исчисление функции одной переменной
(Тема 3.3.)
План лекции
Первообразная и неопределенный интеграл и их свойства.
Интегрирование методом подстановки и по частям.
Интегрирование тригонометрических функций.
Определенный интеграл, его основные свойства.
Формула Ньютона-Лейбница
Интеграл с переменным верхним пределом.
Приложения определенного интеграла для вычисления площадей плоских фигур.
Определение: первообразной функции  называется функция F(x), производная от которой равна исходной функции, т.е. F(x) : F’(x) =
называется функция F(x), производная от которой равна исходной функции, т.е. F(x) : F’(x) =  .
.
Операция нахождения первообразной функции является обратной по отношению к нахождению производной.
Пусть  = x3, найти F(x) = ?
= x3, найти F(x) = ? 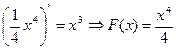 ;
;
Утверждение: если 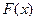 первообразная для
первообразная для  , то
, то 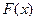 +с тоже первообразная для
+с тоже первообразная для  .
.
Доказательство: 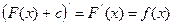
Утверждение: если F1(x) и F2(x) первообразные  , то они отличаются друг от друга на const: F1(x) - F2(x) = с
, то они отличаются друг от друга на const: F1(x) - F2(x) = с
Доказательство: 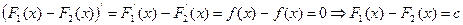
Определение: неопределённым интегралом функции  называется вся совокупность её первообразных.
называется вся совокупность её первообразных.
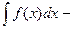 неопределённый интеграл.
неопределённый интеграл.
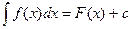 , где
, где 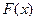 - любая первообразная для
- любая первообразная для  .
.
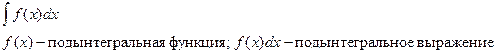
Таблица основных неопределённых интегралов.
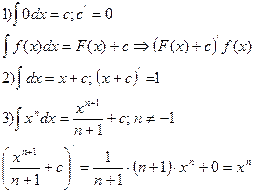
Дата добавления: 2016-06-24; просмотров: 733;
