Плоскость в пространстве

Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.

Разным способам задания плоскости соответствуют различные виды уравнений Таблица

№ п/п	Вид уравнения	Смысл входящих в уравнение коэффициентов	Примечание
	Уравнение плоскости, проходя-щей через данную точку пер-пендикулярно заданному век-тору А(х-х0)+В(у-у0)+С(z-z0)=0	(x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора	Вектор N(А,В,С) называется нормальным вектором плоскости
	Общее уравнение плоскости Ах+Ву+Сz+D=0	D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; х0,y0,z0 – координаты данной точки	Это уравнение получается из уравнения (1) эле-ментарными преобразованиями
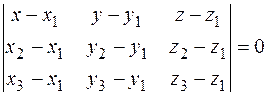
	Уравнение плоскости, проходящей через три заданные точки	М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами	Точки М1, М2, М3 не должны лежать на одной прямой
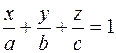
	Уравнение плоскости в отрезках на осях	а,b,c – отрезки, отсекаемые плоскостью от осей координат	аbc≠0

Пусть даны две плоскости a₁ и a₂: a₁: А₁х +В₁у+С₁z+D₁=0,

a₂: А₂х +В₂у+С₂z+D₂=0.

Угол между двумя плоскостями определяется как .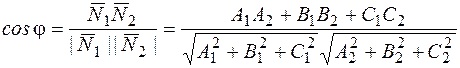

Условие перпендикулярности двух плоскостей:

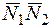=0, то есть 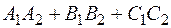=0.

Условие параллельности двух плоскостей:

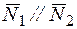или .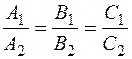

Расстояние от точки до плоскости:

,

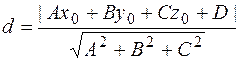где Ах+Ву+Сz+D=0 – заданная плоскость; М(x₀,y₀,z₀) – данная точка.