Система однородных линейных уравнений
Рассмотрим особо частный случай линейной системы, когда свободные члены всех уравнений равны нулю, т.е. систему однородных уравнений:
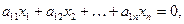
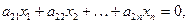 (1)
(1)
…………….
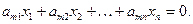
Эта система всегда обладает нулевым или тривиальным решением:
x1=0, x2=0, … , xn=0.
Таким образом, однородная система всегда совместна, и речь может идти лишь о числе её решений: будет ли нулевое решение единственным, или, кроме него, система имеет еще другие, нетривиальные решения.
Теорема 1. Любая система однородных линейных уравнений, в которой число уравнений меньше числа неизвестных, имеет нетривиальные решения.
Теорема 2. Система однородных линейных уравнений с n неизвестными тогда и только тогда имеет нетривиальные решения, когда определитель равен нулю.
Лекция 4 Векторы. Операции над векторами
(Тема 2.1.)
План лекции
Определение вектора.
Модуль вектора.
Координаты вектора.
Операции над векторами (скалярное, векторное и смешанное произведения), свойства.
Геометрический вектор 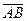 – это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
– это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
Длиной вектора (модулем) называют длину отрезка АВ. Векторы обозначают как 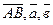 , а их длины
, а их длины 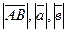 .
.
Два вектора называются равными, если они имеют равные длины и одинаковое направление.
Вектор, начало и конец которого совпадают, называется нулевым.
Произведением вектора 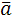 на некоторое число αÎR называется вектор, длина которого равна длине вектора
на некоторое число αÎR называется вектор, длина которого равна длине вектора 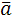 , умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора
, умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора 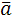 , если α>0, и противоположно ему, если α<0.
, если α>0, и противоположно ему, если α<0.
Суммой нескольких векторов называется вектор, проведенный из начала первого вектора в конец последнего при условии, что начало каждого последующего вектора совмещается с концом предыдущего.
Проекцией вектора 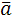 на ось Ох называется число, равное длине вектора
на ось Ох называется число, равное длине вектора 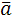 , умноженной на косинус угла между вектором
, умноженной на косинус угла между вектором 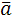 и положительным направлением оси Ох.
и положительным направлением оси Ох.
Радиусом-вектором точки М называется вектор 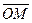 соединяющий начало координат с этой точкой.
соединяющий начало координат с этой точкой.
Единичные векторы координатных осей 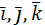 называются ортами.
называются ортами.
Углы α, β, γ между вектором 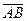 и положительными направлениями осей координат называются направляющими, при этом для вектора
и положительными направлениями осей координат называются направляющими, при этом для вектора  с координатами Х, Y, Z
с координатами Х, Y, Z 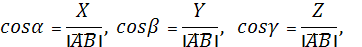 причем
причем 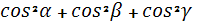 =1.
=1.
Если векторы  и
и  заданы своими координатами как
заданы своими координатами как 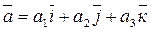 и
и 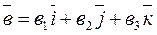 , то координаты вектора ma +nb будут равны: {ma1 +nb1, ma2+nb2, ma3+nb3}, а вектор ma +nb=( ma1 +nb1)
, то координаты вектора ma +nb будут равны: {ma1 +nb1, ma2+nb2, ma3+nb3}, а вектор ma +nb=( ma1 +nb1) 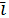 +(ma2+nb2)
+(ma2+nb2) 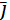 +(ma3+nb3)
+(ma3+nb3) 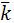 .
.
Дата добавления: 2016-06-24; просмотров: 573;
