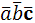Скалярное произведение двух векторов
 |  |  | |||
|
|
|

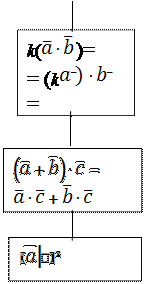 | |||||
 | |||||
 | |||||
Векторное произведение двух векторов
 |  |  | |||
|
|
|

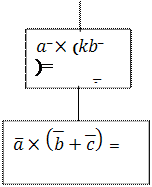 | |||||
 | |||||
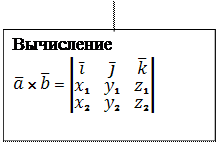 | |||||
Смешанное произведение трех векторов
 |  |  | |||
|
|
|

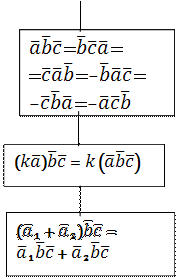 | |||||
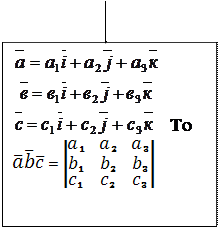 | |||||
 | |||||
Лекция 5 Прямая на плоскости и в пространстве. Уравнение плоскости
(Тема 2.2.)
План лекции
Уравнение прямой на плоскости: с угловым коэффициентом, в канонической и параметрической форме, уравнение прямой проходящей через две данные точки.
Угол между прямыми.
Уравнение прямой в пространстве.
Уравнение плоскости в пространстве.
Уравнением линии на плоскости ХОУ называется такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Простейшей из линий является прямая.
Разным способам задания прямой соответствуют в прямоугольной системе координат различные виды ее уравнений
Таблица
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечания |
| Уравнение с угловым коэффициентом y=kx+b | k – тангенс угла a наклона прямой к положительному направлению оси ОХ; b – отрезок, отсекаемый прямой от оси ОY | a≠π/2 | |
| Общее уравнение прямойАх+Ву+С=0 | А,В – координаты вектора, перпендикулярного прямой (нормального вектора) N. | А,В не равны нулю одновременно | |
| Уравнение прямой, про-ходящей через данную точку в данном направ-ленииу-у0=k(х-х0 ) | т.М(х0,у0) – заданная точка; k – угловой коэффициент прямой | При различных k уравнение называется уравнением пучка прямых с центром в точке М(х0,у0) | |
Уравнение прямой, проходящей через две заданные точки 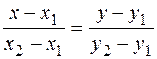
| т.М1(х1,у1), т.М2(х2,у2) – заданные точки | ||
Уравнение прямой в отрезках на осях х 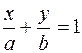 . .
| а,b – отрезки, отсекаемые прямой от координатных осей ОХ и ОY соответственно | а≠0, b≠0 | |
Уравнение прямой, проходящей через заданную точку параллельно заданному вектору 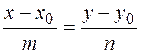
| т.М0(х0,у0) – заданная точка; m,n – координаты вектора, параллельного искомой прямой ( направляющего век-тора) 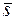
| Такое уравнение часто называют каноническим | |
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору А(х-х0)+В(у-у0)=0 | т.М0(х0,у0) – заданная точка, А,В – координаты нормального вектора искомой прямой 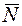
|
Дата добавления: 2016-06-24; просмотров: 595;

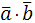 =|
=| 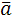 ||
|| 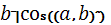
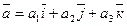 |
| 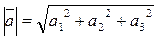
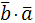
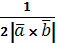
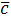 , длина которого численно равна площади параллелограмма, построенного на векторах
, длина которого численно равна площади параллелограмма, построенного на векторах 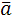 и
и 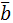 и направлен так, что кратчай-ший поворот от
и направлен так, что кратчай-ший поворот от 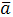 к
к 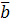 видится против часовой стрелки
видится против часовой стрелки
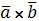 =
= 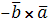
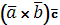 =
= 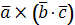
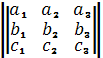
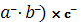 =
=