Декартово произведение множеств

Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b – второй координатой (компонентой) пары.

Пары (а; b) и (с; d) равны в том и только в том случае, когда а = с и b = d.

В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая компонента – множеству В. Если мы перечислим все такие пары, то получим множества:

{(1; 3), (1; 5) (2; 3), (2; 5), (3; 3), (3; 5)}.

Видим, что, имея два множества А.и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.

Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:

А х В = {х; у) / х ∈ А и у∈ В}.

Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А х В и В х А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.

Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:

(А∪В) х С = (А х С) ∪ (В х С),

(А / В) х С = (А х С) / (В х С).

Доказывать эти свойства мы не будем, но проверить их можно на конкретных примерах.

Выясним теперь, как можно наглядно представить декартово произведение множеств.

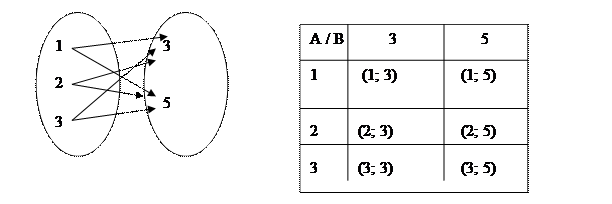
Если множества А и В конечны и содержат небольшое количество элементов, то его можно изобразить при помощи графа или таблицы. Например, декартово произведение множеств

А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке.

А В

Декартово произведение двух числовых множеств (конечных и бесконечных) можно изобразить на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение выше названных множеств на координатной плоскости будет выглядеть так:

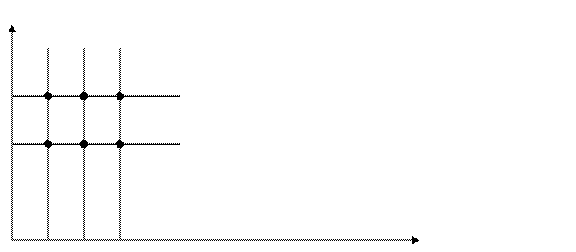
1 2 3

Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В – на оси Оу.

Такой способ наглядного изображения декартова произведения множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.

В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367 – это упорядоченный набор из трех элементов, а запись слова «математика» - это упорядоченный набор из 10 элементов.

Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10.

Рассматривают в математике и декартово произведение трех, четырех и вообще n множеств.

Определение. Декартовым произведением множеств А₁, А₂, …, Аn называется множество всех кортежей длины n, первая компонента которых принадлежит множеству А₁, вторая – множеству А₂, …, n-я - множеству Аn.

Декартово произведение множеств А₁, А₂, …, Аn обозначают так:

А₁ х А₂ х …х Аn.