Отношения между множествами. Подмножество. Равные множества. Универсальное множество. Круги Эйлера. Числовые множества.

В математике изучают не только те или иные множества, но и отношения, взаимосвязи между ними. Например, нам известно, что все натуральные числа являются целыми. Понятие множества позволяет обобщить конкретные случаи взаимосвязи между различными совокупностями, позволяет посмотреть на них с единой точки зрения.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.

Например, если А ={a, b, c, d, e}, В = {b, d, k, m}, С = {х, у, z}, то можно утверждать, что множества А и В пересекаются, а множества А и С, В и С не пересекаются.

Рассмотрим множества А ={a, b, c, d, e} и В = {с, d, е}. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. В этом случае говорят, что множество В включается в множество А или что множество В является подмножеством А и пишут: В⊂А.

Определение: Множество В является подмножеством А, если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.

Верно: ∅⊂А и А ⊂А. В этом случае множества ∅ и А называют несобственными.

Образуем, например, все подмножества множества А = {2, 3, 4}. Среди них будут одноэлементные подмножества: {2}, {3},{4}, двухэлементные {2, 3}, {2, 4}, {3, 4}, а также само множество А и пустое множество ∅. Таким образом, данной трехэлементное множество А имеет 8 подмножеств.

Доказано, что если множество содержит n элементов, то у него 2ⁿ различных подмножеств.

Если рассматриваются подмножества одного и того же множества U, то в этом случае U называют универсальным. Так множество четырехугольников универсально для множества ромбов, квадратов, трапеций, прямоугольников, параллелограммов.

Определение. Множества А и В называются равными, если А⊂В и В⊂А.

Из определения следует, что равные множества состоят из одних и тех же элементов и что порядок записи элементов множества не существен.

Отношения между множествами наглядно представляют при помощи особых чертежей, называемых кругами Эйлера. Возможны следующие отношения между двумя множествами:

А В А В А=В А В

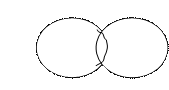
а) б) в) г) д)

Пересекаются - а); В⊂А - б), А⊂В - в), А = В - г), А и В не пересекаются

Понятие подмножества является обобщением понятия части и целого, которые осваивают младшие школьники, выполняя разные задания. Например: «Назови среди данных чисел четные», «Среди данных четырехугольников найди прямоугольники».