Определители n-го порядка
Определение. Определителем n-го порядка называется число, записываемое в виде:
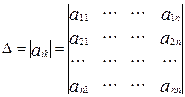
Вычисляется как сумма произведений элементов какого-либо столбца (строки) на их алгебраические дополнения, т.е. вычисление определителя n-го порядка сводится к вычислению n определителей порядка (n-1).
Все перечисленные выше свойства относятся к определителям любого порядка (также определение минора и алгебраического дополнения).
Ранг матрицы.
Определение. Пусть А – некоторая матрица. Выделим в ней произвольно k строк и k столбцов. Определитель k-того порядка, составленный из элементов, находящихся на пересечении выделенных строк и столбцов, называется минором k-того порядка матрицы А. Пир этом строки и столбцы этого определителя должны быть расположены относительно друг друга в том же порядке, что и в матрице.
Каждый элемент матрицы будем рассматривать как её минор первого порядка.
Пример. Составить всевозможные миноры третьего порядка матрицы
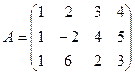
и какой-нибудь минор второго порядка.
Решение. Для получения миноров третьего порядка надо выделить все три строки матрицы и какие-нибудь три её столбца. Таких миноров будет четыре:
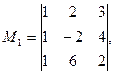
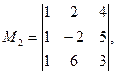
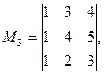
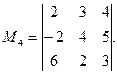
Выделим теперь в той же матрице первую и третью строки и второй и третий столбцы. Элементы, стоящие на пересечении этих строк и столбцов, образуют минор второго порядка рассматриваемой матрицы: 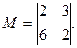
Рангом матрицы назовём наивысший порядок её минора, отличного от нуля.
Другими словами, целое число r > 0 называется рангом матрицы, если среди миноров r-того порядка этой матрицы есть хотя бы один, отличный от нуля, а все миноры более высокого порядка равны нулю.
Пример. В предыдущем примере миноров порядка выше третьего данная матрица не имеет, все миноры третьего порядка равны нулю, а минор М второго порядка 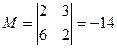 отличен от нуля. Поэтому ранг её равен двум: r (A)=rang A=2.
отличен от нуля. Поэтому ранг её равен двум: r (A)=rang A=2.
Вычисление ранга матрицы непосредственно по его определению, вообще говоря, громоздко так как приходится вычислять большое число миноров. Рассмотрим другой способ, основанный на приведении матрицы к ступенчатому виду.
Матрицу А называют ступенчатой, если:
а) любая её строка имеет хотя бы один отличный от нуля элемент;
б) первый отличный от нуля элемент каждой её строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.
Пример. Матрицы
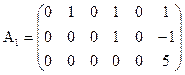 и
и 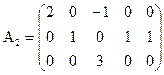
являются ступенчатыми (или имеют ступенчатый вид), а матрицы
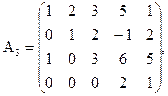
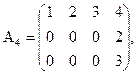
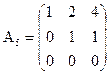
ступенчатыми не являются.
Назовём элементарными преобразованиями матрицы следующие преобразования её строк:
1) перестановку двух каких-нибудь строк;
2) умножение элементов какой-нибудь строки на чисо, отличное от нуля;
3) прибавление к элементам какой-нибудь строки соответствующих элементов другой строки, умноженных на некоторое (одно и тоже) число.
Поясним эти преобразования примером:
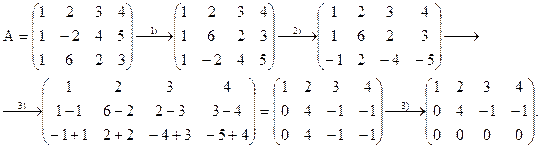
Способ вычисления ранга произвольной матрицы будет вытекать непосредственно из следующих утверждений:
1). При элементарных преобразованиях и отбрасывании нулевой строки (т. е. строки, у которой все элементы равны нулю) ранг матрицы не изменяется.
2). Всякую ненулевую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований и выбрасывания нулевых строк.
3). Ранг ненулевой матрицы равен числу строк ее ступенчатого вида.
Пример. Вычислить ранг матрицы А путём приведения её к ступенчатому виду.
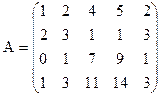
Проведём следующие элементарные преобразования:
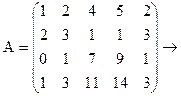
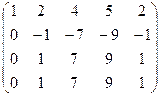
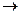
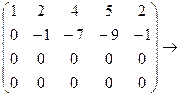
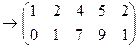 .
.
Отсюда видно (так как 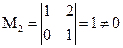 ), что ранг данной матрицы А равен двум.
), что ранг данной матрицы А равен двум.
Обратная матрица
Пусть А – квадратная матрица n-го порядка.
E – единичная матрица того же порядка .
Матрица B называется правой обратной к A, если AB = E
Матрица С называется левой обратной к A, если CA = E
Очевидно, что матрицы B и C – тоже квадратные. Покажем, что если B и C существуют, то они совпадают между собой.
AB = E CA = E
C = CE = C(AB) = (CA)B = EB = B
Теорема. Для того, чтобы к матрице A существовали левая и правая обратные матрицы, необходимо и достаточно, чтобы 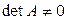
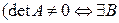 и
и 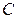 ).
).
Определение: Квадратная матрица 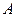 , определитель которой отличен от нуля, называется невыроженной.
, определитель которой отличен от нуля, называется невыроженной.
Если 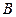 - обратная к
- обратная к 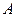 и
и 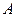 - обратная к
- обратная к 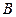 , обозначим
, обозначим 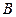 =
= 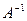
Дата добавления: 2016-06-24; просмотров: 1109;
