Основные операции над матрицами и их свойства.
Определение. Две матрицы называются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают.
1. Сложение матриц (только одинаковых порядков).
A= 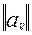 ; i=
; i= 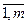 ; j=
; j= 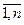 ;
;
B=  ; i=
; i= 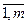 ; j=
; j= 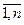 ;
;
Суммой матриц А и Вназывается матрица C= 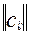 , имеющая те же порядки, что и слагаемые матрицы, элементы которой
, имеющая те же порядки, что и слагаемые матрицы, элементы которой  :
:
 =
=  +
+ 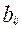 , i=
, i= 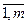 , j=
, j= 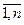 .
.
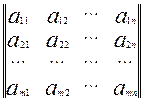 +
+ 
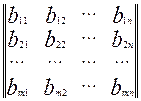 =
= 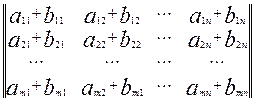 .
.
Из определения операции сложения матриц следует, что она обладает свойствами операций сложения вещественных чисел:
1) A+B=B+A-коммутативность
2) (A+B)+C=A+(C+B) – ассоциативность
2. Умножение матриц на число.
Пусть l -вещественное число.
A= 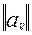 ; i=
; i= 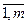 ; j=
; j= 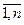 ;
;
Произведением матрицы A на число l называется матрица C= 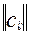 ; i=
; i= 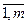 ; j=
; j= 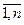 , элементы которой:
, элементы которой: 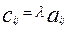 C=lA=Al
C=lA=Al
Свойства операции умножения на число:
1). (λµ)А = λ(µА) – ассоциативность по отношению к вещественному множителю.
2). λ(А+В) = λА+λВ – дистрибутивность по отношению к сложению матриц.
3). (λ+µ)А = λА+µА – дистрибутивность по отношению к сложению чисел.
3. Разность матриц А и В вводится следующим образом:
С = А – В = А + (-1)В,
т. е. используя уже определенные операции сложения и умножения на число.
4. Перемножение матриц.
Пусть А = ║aij║, 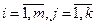 (m×k)
(m×k)
B = ║bij║ , 
 (k×n)
(k×n)
Определение. Две матрицы называются сцепленными, если число столбцов первой матрицы равно числу строк второй.
Операция перемножения определена только для сцепленных матриц.
Определение. Произведением матрицы А на матрицу В называется матрица
C = ║cij║ , 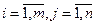 (m×n), элементы которой определяются следующим образом: Cij=
(m×n), элементы которой определяются следующим образом: Cij= 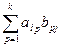
 . Обозначение: С=АВ
. Обозначение: С=АВ
Правило перемножения матриц: элемент cij , стоящий на пересечении i-й строки и j-го столбца матрицы С, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
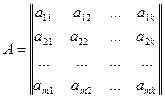


Оба произведения АВ и ВА можно определить лишь в том случае, если число столбцов А совпадает с числом строк В, а число столбцов В – с числом строк А. При этом обе матрицы-произведения С1 и С2 будут квадратными, но различного порядка.
Для того, чтобы оба произведения имели один порядок, необходимо и достаточно, чтобы матрицы А и В были квадратными одного порядка.
Пример:
А= 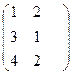 В =
В = 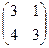 С=АВ=
С=АВ= 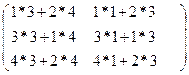 =
= 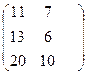
Из определения произведения матриц вытекает следующие свойства произведения матриц:
1. (АВ)С=А(ВС) -- ассоциативность
2. (А+В)С=АС+ВС или А(В+С)=АВ+АС – дистрибутивностьотносительно сложения матриц
(Это свойство вытекает из определения и из формулы сложения)
3. В общем случае АВ≠ВА, умножение матриц не коммутативно.
Произведение матриц не коммутативно и для квадратных матриц одного порядка:


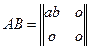 , а
, а 
Но есть частные случаи, когда произведение матриц коммутативно.
Среди квадратных матриц выделим класс диагональных матриц (все элементы вне главной диагонали равны нулю).
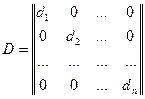
Если все di=d, то для любой квадратной матрицы А порядка n : АD=DA
Доказательство: Пусть Cij и Cij/ - элементы матриц АD и DA => Cij=aij∙dj=aij∙d, Cij/=di∙aij=daij =>
=> Cij= Cij/
d=1 – единичная матрица ≡ Е (аналог единицы при перемножении вещественных чисел)
d=0 – нулевая матрица ≡ О (нулевая матрица может быть и не квадратной)
АЕ=ЕА АО=ОА.
Определители
Квадратной матрице можно поставить в соответствие число, называемое определителем.
Определение: Пусть дана квадратная матрица из четырех чисел.
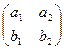 .
.
Число а1b2 - а2b1 называется определителем второго порядка, соответствующим данной матрице.
Обозначается : 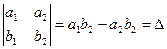
Числа а1, а2, b1, b2 называются элементами определителя.
Элементы а1, b2 лежат на главной диагонали определителя, а элементы а2, b1 - на побочной диагонали.
а1 и а2 – элементы первой строки.
b1 и b2 - элементы второй строки.
а1 и b1 - элементы первого столбца.
а2 и b2 – элементы второго столбца.
Пусть дана квадратная матрица из девяти чисел: a11 a12 … a33 :
А= 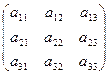
Определителем третьего порядка, соответствующим матрице А, называется число 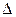 =
= 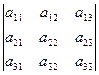 = a11 a22 a33 + a12 a23 a31 + a13 a21 a32 –
= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 –
- a13 a22 a31 - a11 a23 a32 - a12 a21 a33 .
Число aij называется элементом определения, при этом первый индекс – i – указывает номер строки, а второй – j - номер столбца, которым принадлежит данный элемент. Говорят, также, что элемент aij находится на пересечении i-й строки и j-го столбца.
Элементы a11 a22 a33 – образуют главную диагональ определителя, а a13 a22 a31 – побочную диагональ.
Правила вычисления определителя 3-го порядка:
1. Правило Саррюса:


Нужно взять сумму произведений трех элементов, зачеркнутых прямыми. При этом три произведения, соответствующие прямым, параллельным главной диагонали, берутся со знаком (+), а три произведения, соответствующих прямым, параллельным побочной диагонали, берутся со знаком (-).
2. Номера строк располагаются в порядке возрастания превого индекса, а номера столбцов – перестановки чисел 123:
123, 231, 312 | 321, 132, 213.
3. Правило треугольника.
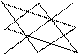

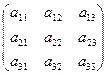
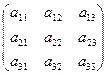
(со знаком +) (со знаком -)
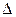 = a11 a22 a33 + a12 a23 a31 + a13 a21 a32 - a13 a22 a31 - a23 a32 a11 – a33 a12 a21
= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 - a13 a22 a31 - a23 a32 a11 – a33 a12 a21
Дата добавления: 2016-06-24; просмотров: 1058;
