Свойства определителей
Свойство 1. Величина определителя не изменяется, если все его строки заменить столбцами с тем же номером.
 =
= 
(Для доказательства достаточно расписать оба определителя и сравнить)
Свойство 1 означает равноправность строк и столбцов определителя.
Свойство 2. Перестановка двух строк (или двух столбцов) равносильна умножению определителя на (-1).
Свойство 3. если определитель имеет две одинаковые строки (или столбца), то он равен 0.
Согласно свойству 2 при перестановке двух одинаковых строк знак должен поменяться, т.е. 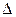 = -
= - 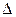
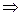 2
2 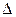 = 0
= 0 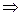
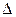 =0.
=0.
Свойство 4. Умножение всех элементов одного столбца или строки на некоторое число  , не равное 0, равносильно умножению определителя на
, не равное 0, равносильно умножению определителя на  . Иными словами, общий множитель всех элементов некоторой строки или столбца можно вынести за знак определителя.
. Иными словами, общий множитель всех элементов некоторой строки или столбца можно вынести за знак определителя.




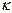 а
а  а
а  а
а  а
а  а
а  а
а 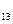
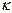 а
а 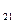 а
а  а
а  =
= а
а 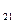 а
а  а
а 
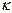 а
а  а
а 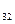 а
а 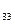 а
а  а
а 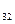 а
а 
Для доказательства заметим, что определитель выражается в виде суммы, каждый член которой содержит один и только один элемент из каждой строки и каждого столбца.
Свойство 5. Если все элементы некоторого столбца или строки равны 0,то определитель равен 0.
(Доказательство: это свойство есть частный случай предыдущего).
Свойство 6. Если соответствующие элементы двух строк или столбцов пропорциональны, то определитель равен 0.




а 
 а
а  а
а  а
а  а
а  а
а 
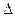 = а
= а 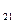
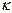 а
а 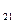 а
а  =
= а
а 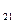 а
а 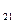 а
а  =
= 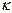 ×0=0. (по свойству 3 и 4)
×0=0. (по свойству 3 и 4)
а 
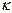 а
а  а
а 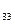 а
а  а
а  а
а 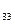
Свойство 7. Если каждый элемент n-го столбца (или n-ой строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-ом столбце (n-ой строке) имеет первые слагаемые, а другой - вторые. Элементы, стоящие на остальных местах этих определителей - одинаковые.
(Проверить применением правила треугольника к правой и левой частям).
Свойство 8. Если к элементам некоторого столбца (или строки) прибавить соответствующие элементы другого столбца (или строки), умноженные на некоторый общий множитель  , отличный от 0, то величина определителя при этом не изменится.
, отличный от 0, то величина определителя при этом не изменится.
Свойство вытекает из 7 и 6. Это свойство позволяет при вычислении определителя больше третьего порядка понижать порядок определителя.
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 |  | ||||||||||
а  +
+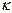 а
а  а
а  а
а 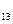 а
а  а
а  а
а 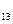
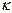 а
а  а
а  а
а 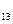

 а
а 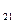 +
+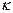 а
а  а
а  а
а  = а
= а 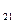 а
а  а
а  +
+ 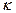 а
а  а
а  а
а  =
= 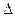 +
+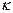 ×0 =
×0 = 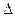
а  +
+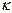 а
а 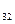 а
а 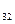 а
а 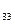 а
а  а
а 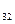 а
а 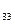
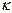 а
а 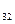 а
а 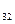 а
а 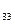
Для рассмотрения дальнейших свойств определителей введем понятия минора и алгебраического дополнения.
Минором элемента определителя называется определитель, полученный из данного путём вычеркивания строки и столбца, на пересечении которых находится этот элемент.
Алгебраическое дополнение элемента определителя равняется минору этого определителя, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число - нечётное:  =
= 
 .
.
Свойство 9. Определитель равен сумме произведений элементов какого-либо столбца или строки на их алгебраические дополнения. (Такая сумма называется разложением определителя по элементам строки или столбца).
 =
=
=  +
+ 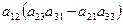 +
+ 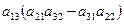 =
= 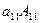 +
+  .
.
А11 - алгебраическое дополнение элемента a  .
.
Свойство 10. Сумма произведений элементов, какого либо столбца (строки) определителя на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.
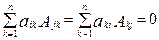 , i
, i 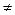 j
j
Доказательство: 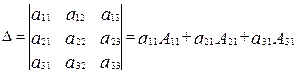
Заменим элементы 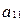
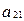
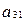 на
на 
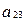
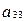 , получим
, получим
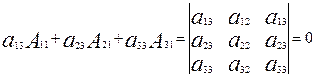 .
.
Аналогично можно записать все суммы.
Дата добавления: 2016-06-24; просмотров: 721;
