Лекция 6 Кривые второго порядка
(Тема 2.3.)
План лекции
Канонические уравнения окружности, эллипса, гиперболы, параболы.
Построение кривых 2-го порядка.
Уравнение вида Ах2+2Вху+Су2+2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
Окружность. Уравнение окружности с центром в точке С(a;b) и радиусом, равным R: 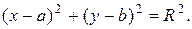
Эллипс. Каноническое уравнение 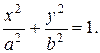
Координаты фокусов: (-с;0) и (с;0), где с= 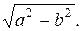
Эксцентриситет: 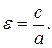 Уравнения директрис:
Уравнения директрис: 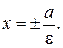
Гипербола. Каноническое уравнение 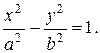
Координаты фокусов: (-с;0) и (с;0), где с= 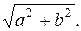
Уравнения асимптот: 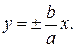
Эксцентриситет: 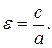 Уравнения директрис:
Уравнения директрис: 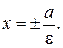
Парабола. Каноническое уравнение 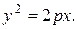
Координаты фокуса: ( 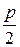 ,0). Уравнение директрисы:
,0). Уравнение директрисы: 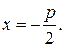
В таблице приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
Таблица
| № п/п | Определение кривой | Вид уравнения | Примечание |
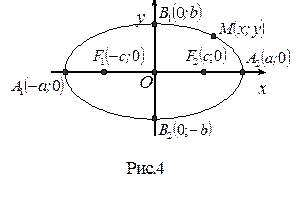 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная
| 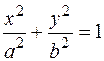 - каноническое уравнение эллипса - каноническое уравнение эллипса
| 2а – большая ось;
2b – малая ось
2с–межфокус-ное; расстояние с2=а2-b2;
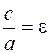 - эксцентриси-тет, 0<e<1.
Т. А1,А2,В1,В2 – вершины эллипса - эксцентриси-тет, 0<e<1.
Т. А1,А2,В1,В2 – вершины эллипса
| |
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная

| 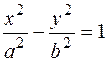 - каноническое уравнение гиперболы - каноническое уравнение гиперболы
| 2а–действи-тельная ось;
2b–мнимая ось;
2с –меж-фокусное расстояние с2=а2+b2;
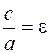 - эксцентри-ситет, e>1.
Точки А1,А2 – вершины гиперболы.
Прямые - эксцентри-ситет, e>1.
Точки А1,А2 – вершины гиперболы.
Прямые 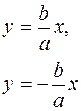 - асимптоты
- асимптоты
| |
| 3. | Парабола - множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
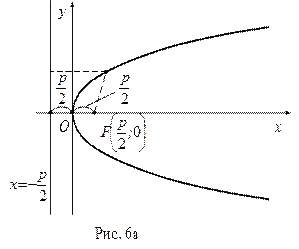 
| у2=2px – каноническое уравнение параболы, симметричной относительно оси ОХ x2=2pу – каноническое уравнение параболы, симметричной относительно оси ОY | F 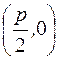 - фокус, - фокус,
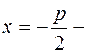 ди-ректриса.
Точка (0;0) – вершина параболы (рис.6а)
F ди-ректриса.
Точка (0;0) – вершина параболы (рис.6а)
F 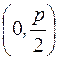 - фокус, - фокус,
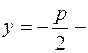 ди-ректриса.
Точка (0;0) – вершина параболы ди-ректриса.
Точка (0;0) – вершина параболы
|
Дата добавления: 2016-06-24; просмотров: 1003;
